複素数平面
ここでは複素数平面の基本事項と,その扱い方について説明しています。基本的な3通りの表し方,$z$などの1文字表記,$x+yi$などの直交形式,$r(\cos\theta+i\sin\theta)$などの極形式について,それぞれの特性を理解して使い分けられるようにしていきましょう。また,複素数について虚数と実数の違いを理解し,絶対値や共役複素数の扱いをマスターしましょう。
複素数

複素数の相等

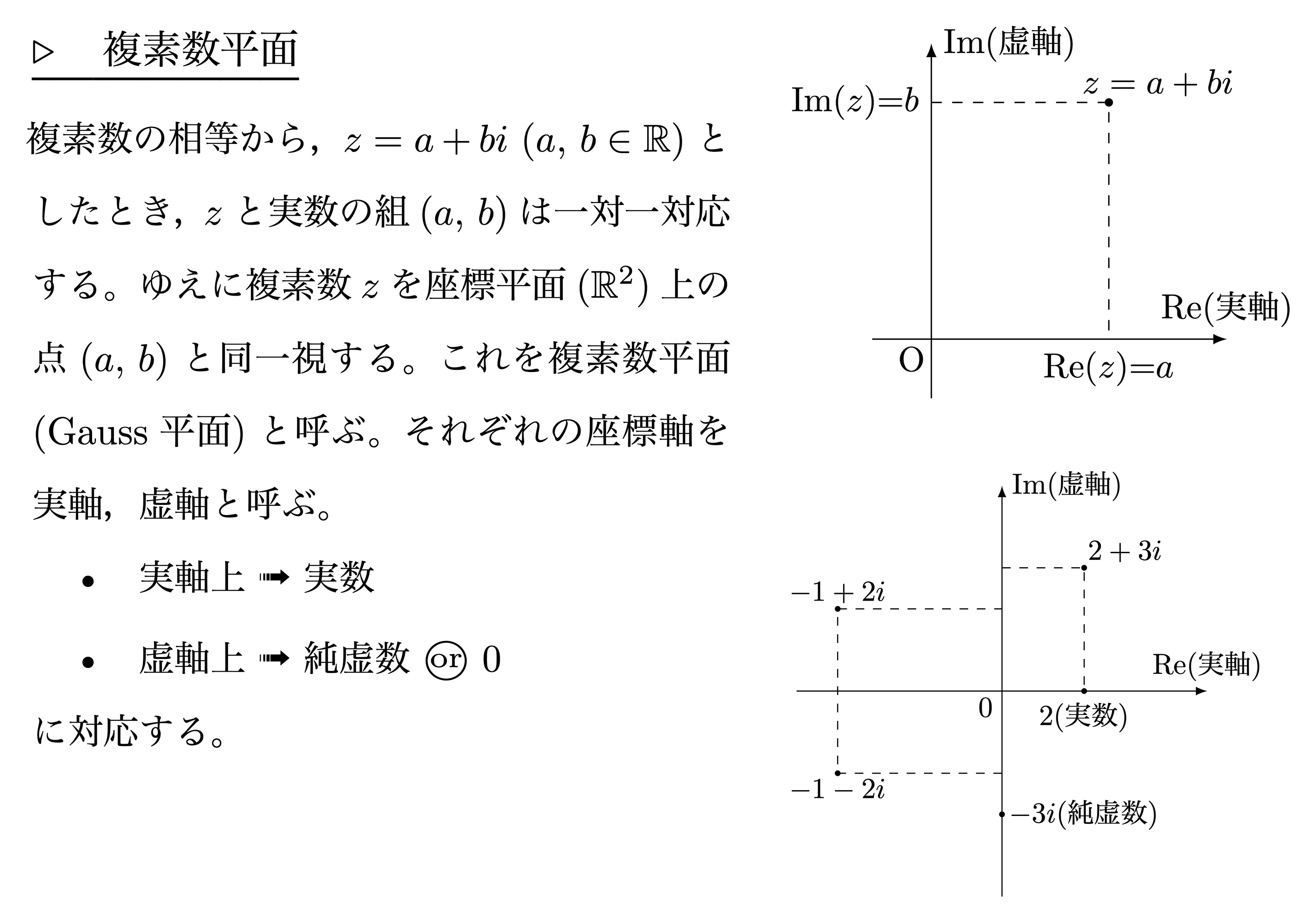
複素数平面
共役複素数

共役複素数の方程式

実数条件・純虚数条件

絶対値

複素数の平方完成

代数学の基本定理

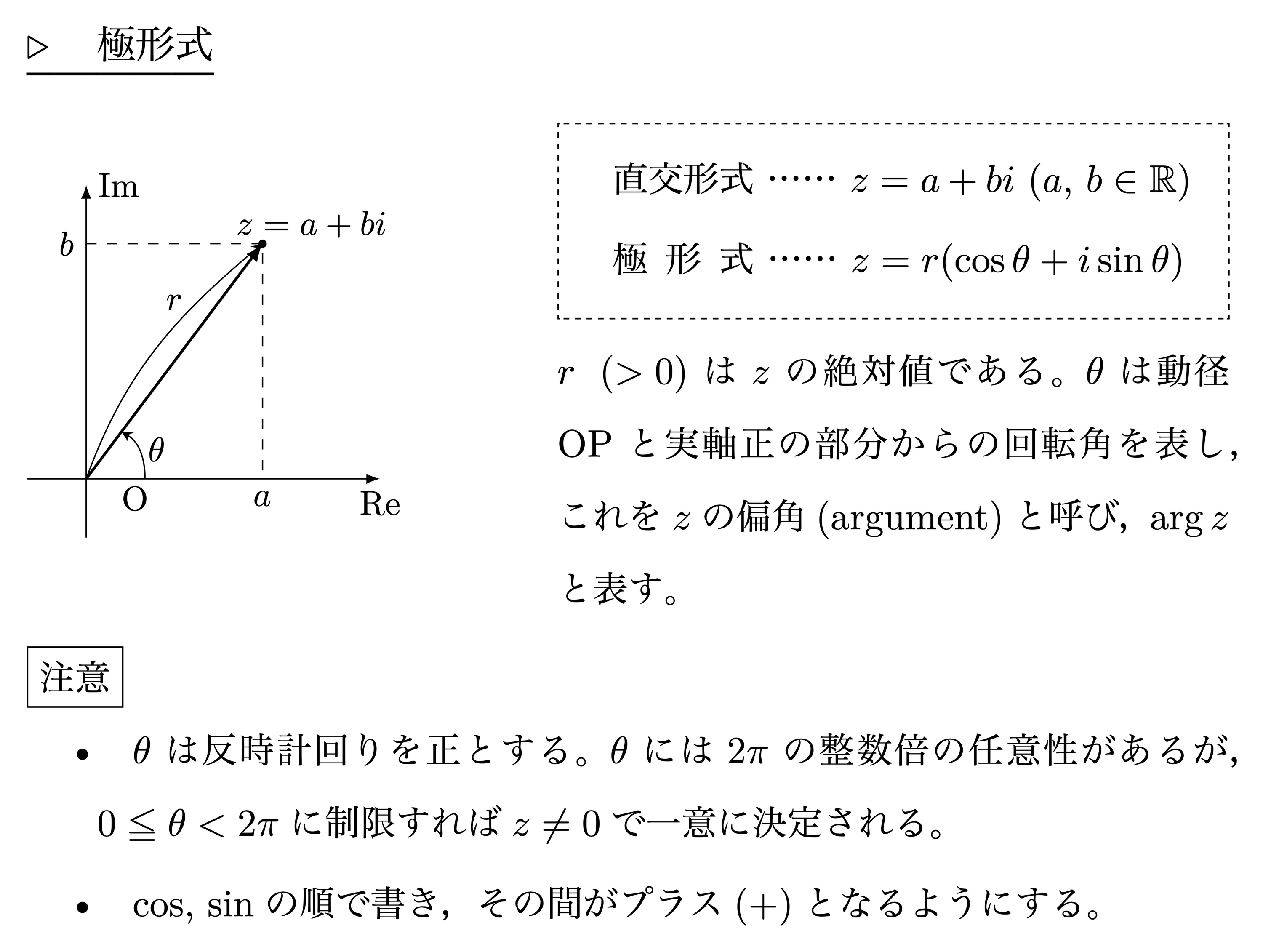
極形式
偏角と絶対値の関係

複素数平面の解法

ド・モアブルの定理
複素数の表記における極形式の最も効果的なワザとして,ド・モアブルの定理があります。基本的な使い所として,複素数の$n$乗の計算,$n$乗根の計算があります。また,このド・モアブルの定理に加えて,$n$乗/$n$乗根の扱いや絶対値が1の複素数の扱いには特徴がありますので,問題文の中から解答の流れを掴むために覚えておきましょう。
ド・モアブルの定理

n乗の扱い

n乗根の扱い

1のn乗根の性質

|z|=1の複素数の性質

三角関数の和

複素数平面上の図形
図形問題の扱い方としてベクトルを用いることがよくあると思いますが,そのベクトルを複素数平面と対応させることにより,解答の幅が広がります。まずは,複素数平面において垂直・平行・回転の扱いを覚えた上で,複素数平面で対応可能な図形問題としては,
- 三角形の形状決定 …… 二辺比狭角
- 円
- 直線
- 4点が同一円周上にある条件 …… 共円条件
が挙げられます。また,本格的な幾何の問題に複素数を導入する際は,回転の中心をうまく定めることが重要です。
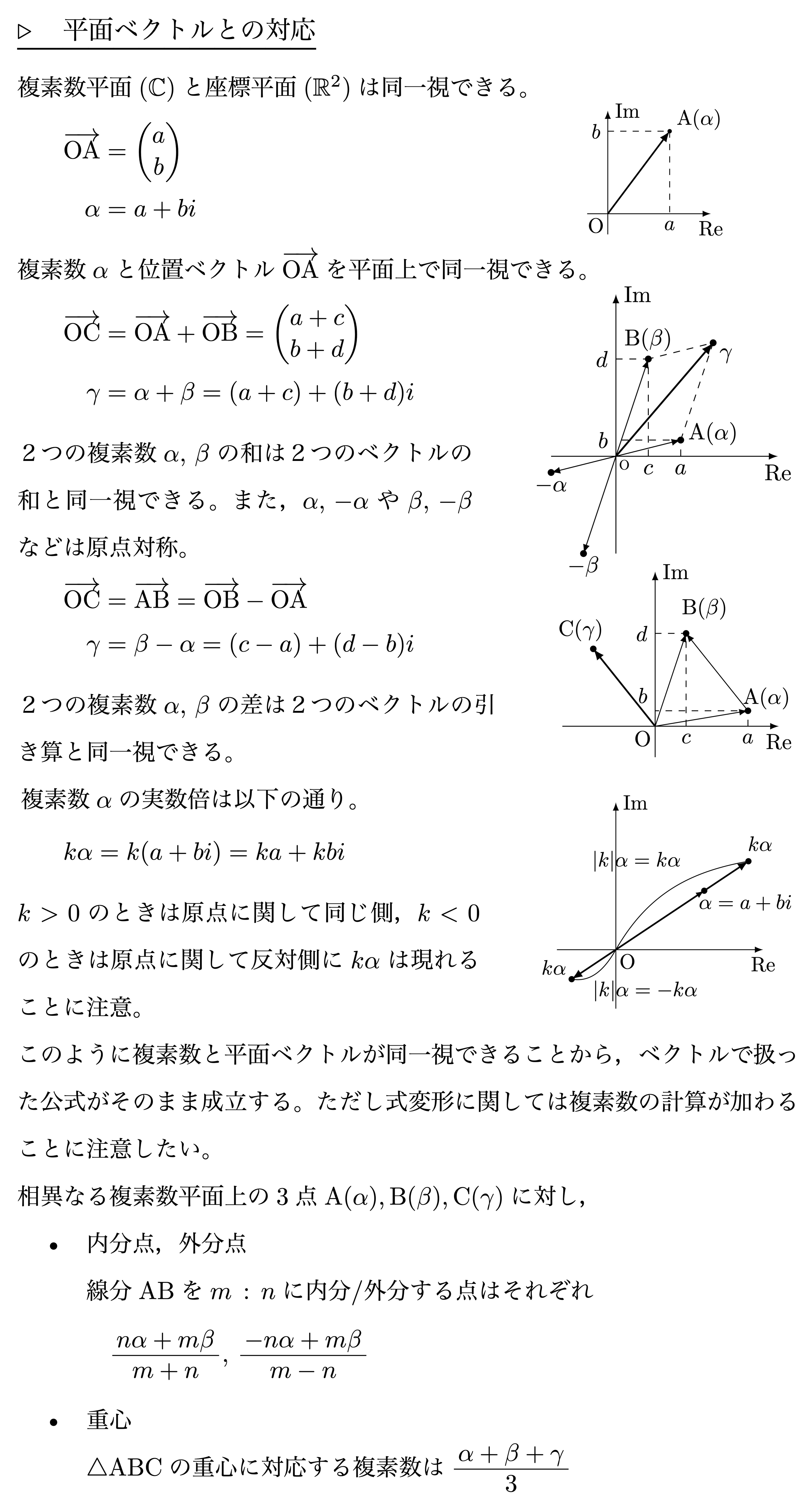
平面ベクトルとの対応
垂直・平行条件

平面上の回転

三角形の形状決定

直線の方程式

円の方程式

初等幾何への応用

共円条件

複素数平面上の変換
上記の複素数平面による図形問題の扱いの発展として,写像$f$によって点$z$の集合(軌跡)がどのような軌跡(点$w$の集合)を描くかを考える際に,次の5つについて扱うことができます。
- 平行移動
- 対称移動
- 拡大縮小
- 回転移動
- 円に関する反転
これらを組み合わせた一次分数変換は難関校の入試問題で頻繁に出題されます。それ以外の変換については$x+yi$として考えましょう。
変換の扱い方

基本的な変換

対称移動

反転

一次分数変換

さまざまな変換

複素数の不等式
前提として複素数には複素数には大小がないため,複素数を含む不等式は2種類に分けられます。
- 複素数の絶対値の不等式 …… 三角不等式で無理なら$x+yi$とする。
- 実数条件が隠れている …… 実数条件$z=\overline{z}$の利用
複素数の不等式

三角不等式

複素数列
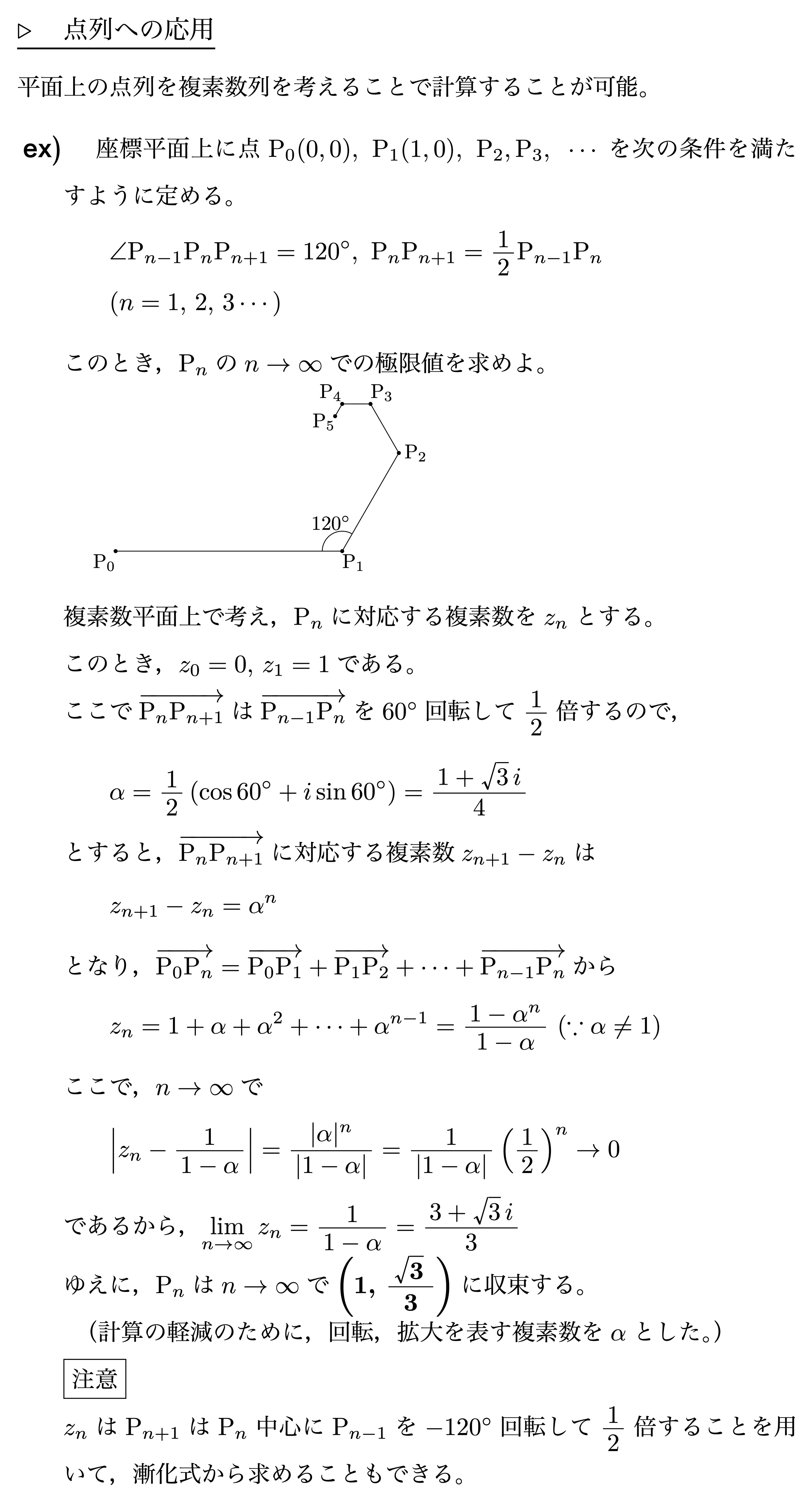
多くの数列の問題は実数ですが,複素数範囲においても同様に考えられます。また,点列の問題においてはベクトル和を考えれば回転について複素数で扱えるとわかるでしょう。
複素数列

点列への応用