二次曲線
二次曲線と呼ばれる,放物線/楕円/双曲線の3つについて,その基本的な定義や漸近線などの性質,円錐曲線としての定義を正確に理解してください。また,二次曲線の問題では接線が絡むものが非常に多いため,接線の扱いをしっかりと覚えましょう。最後に,楕円について円を用いる考え方とそれ以外のパラメータ表示や陰関数表示の使い分けをできるようにしてください。
二次曲線の定義

二次曲線の一般形

焦点からの距離

接線

楕円の扱い
準円

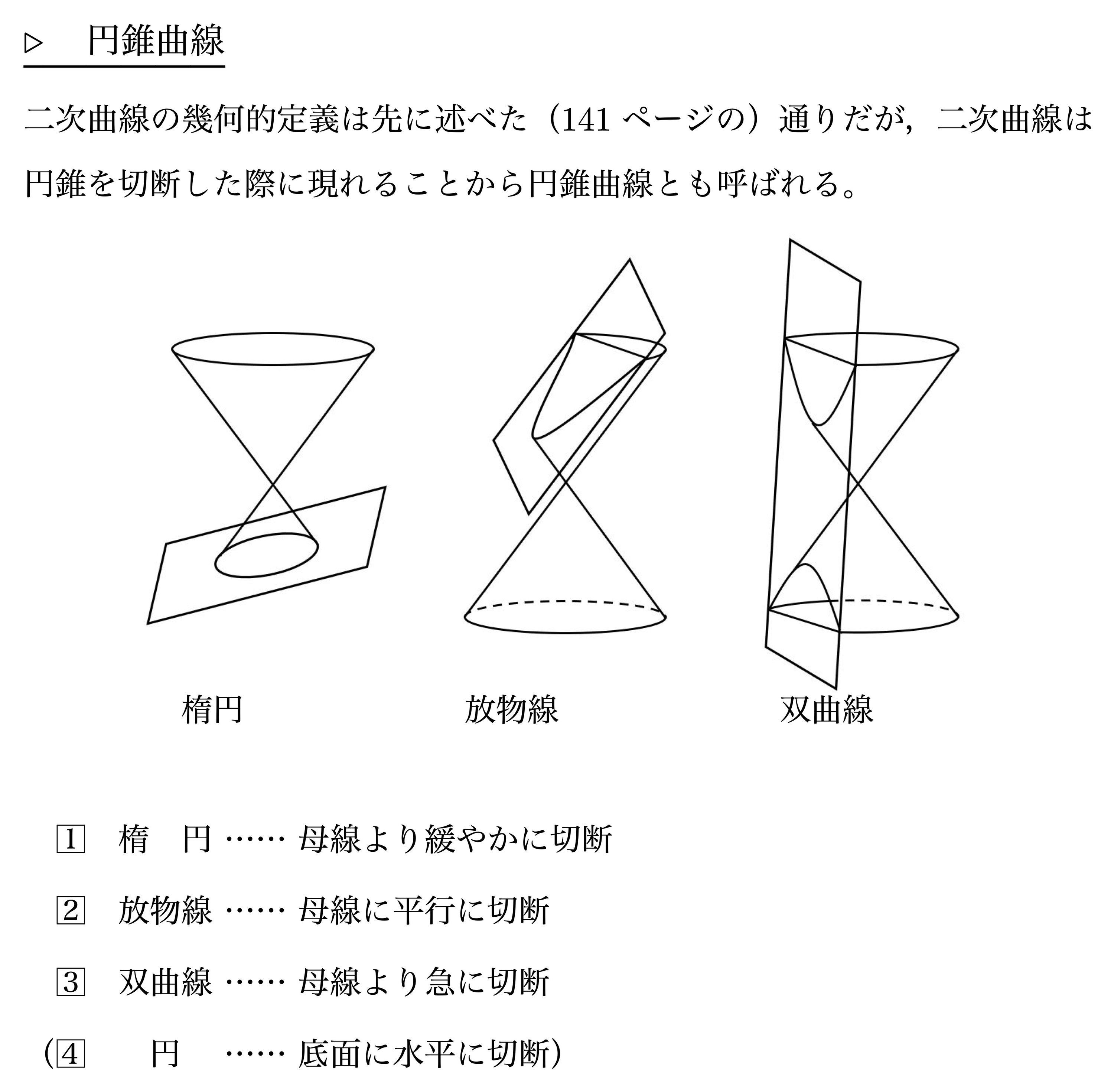
円錐曲線
極座標
平面上の点の表し方として,これまでは直交座標を用いることが多かったものの,別の表し方として極座標表示があります。この極座標上において曲線を表す方程式を極方程式と呼び,しばしば入試で出題される極方程式は扱い方をしっかりと覚えておく必要があります。極方程式の問題は,「$r=f(\theta)$の形」「パラメータ表示の形」のいずれかで出題されます。パラメータ表示の形式で与えられたら,$x=f(\theta)\cos\theta,\ y=f(\theta)\sin\theta$となる$f(\theta)$を見つけねばなりません。解法は次を意識してください。
- 面積 …… 極方程式で扇形近似
- 逆数和 …… 極方程式の利用
- その他 …… $x=r\cos\theta,\ y=r\sin\theta$で$x,y$に戻す
極座標

極方程式

離心率

二次曲線の極方程式

二次曲線の極方程式のグラフ

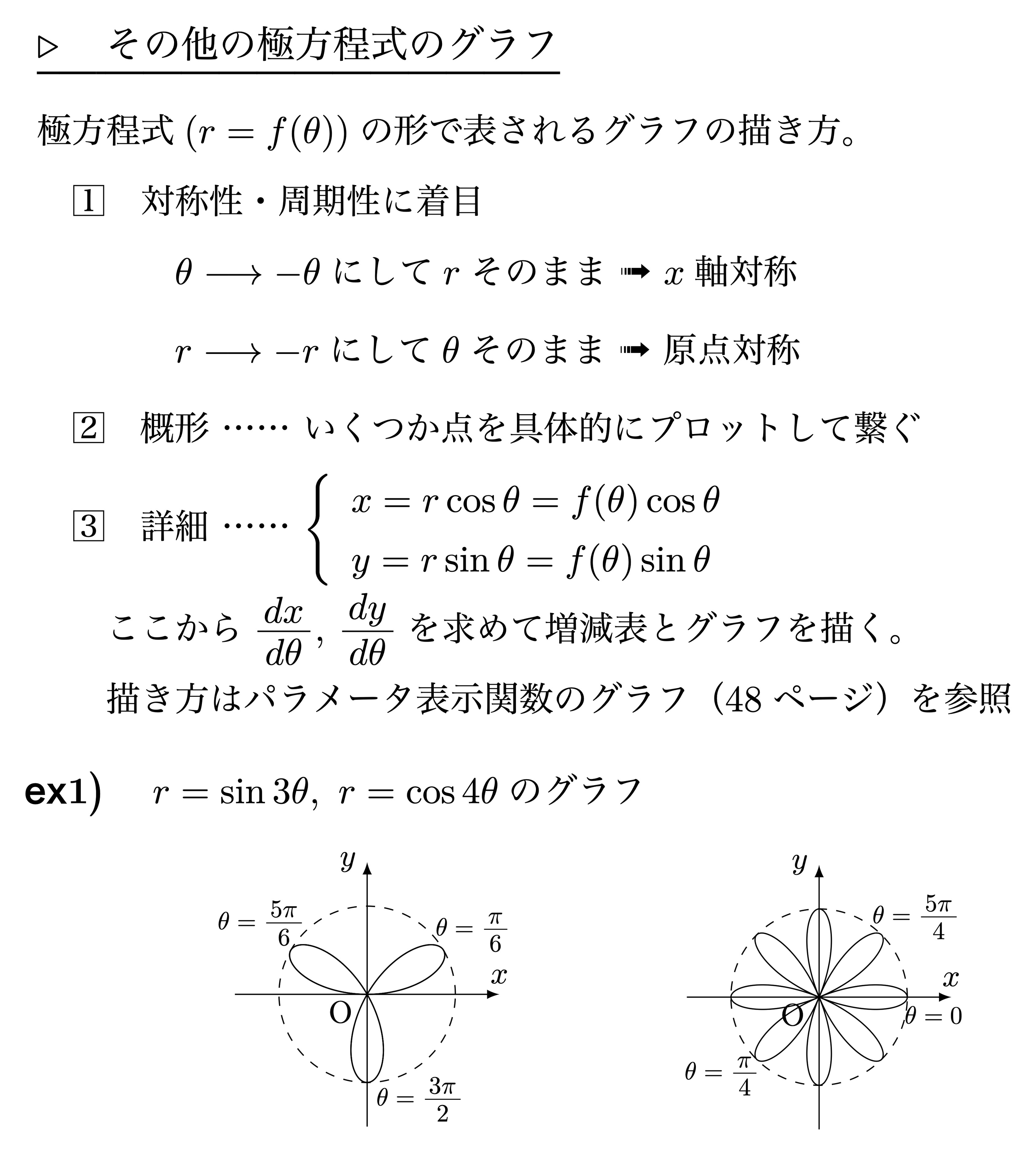
その他の極方程式のグラフ
極方程式で囲まれた部分の面積(扇形近似)
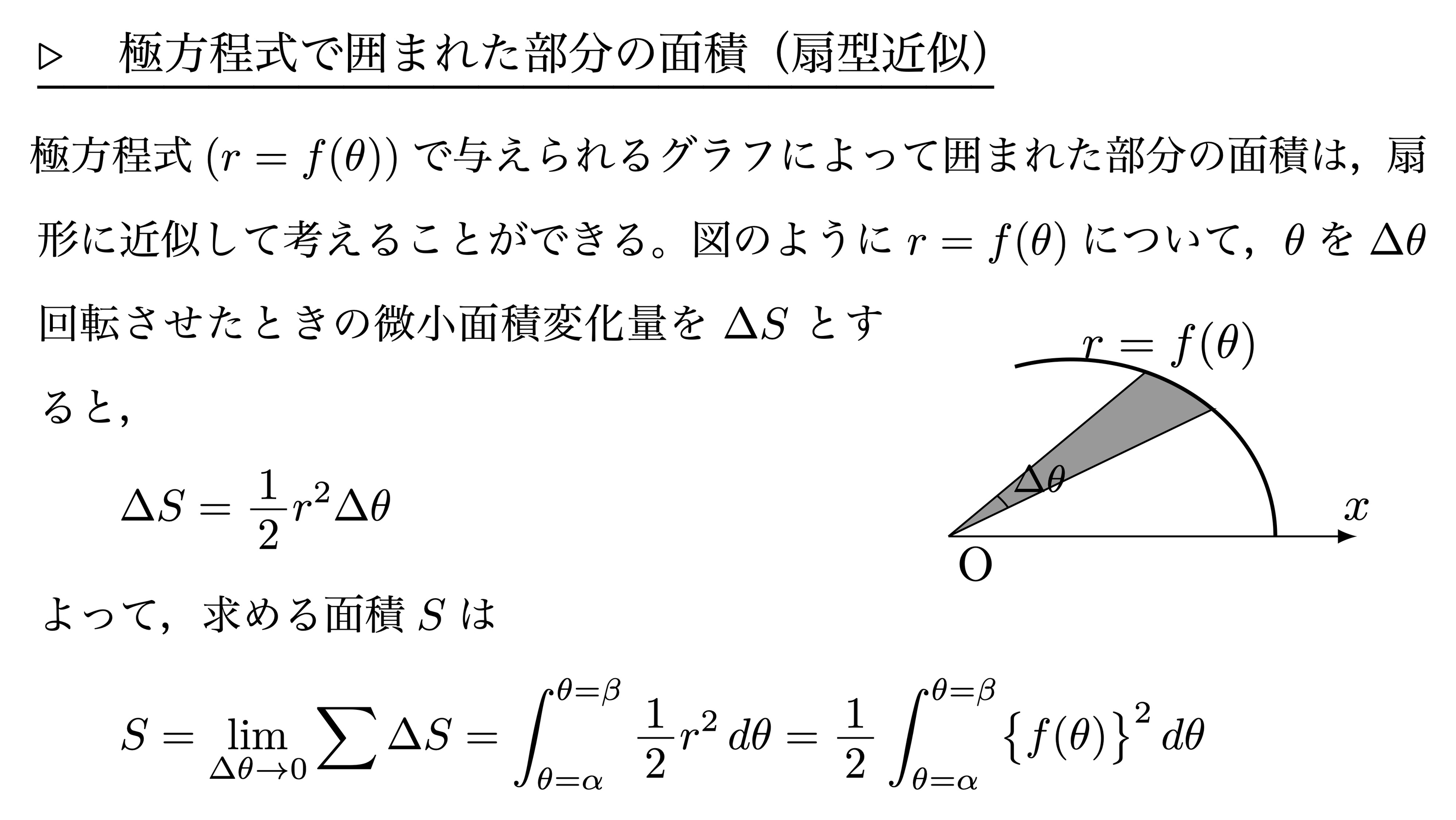
極方程式の利用

パラメータ表示
ここでは有名なパラメータ表示関数をいくつか扱います。覚えていれば有利ですが,式の形に工夫がある問題が出題されることもしばしばですので,パラメータ表示関数の微積分をしっかりと復習して自らグラフや弧長・面積を扱えるようにしましょう。
二次曲線のパラメータ表示

さまざまな曲線