微分係数・導関数の定義
微分係数/導関数の定義についての説明と,微分の表記のまとめを記載しています。微分係数と導関数の違いは,定数か関数かであり,微分の表記はそれぞれのメリット・デメリットを踏まえて使い分けねばなりません。
導関数の定義

微分係数の定義

微分の表記

微分
関数を微分する際には,微分可能性に注意しなければなりません。これは言葉の通り,ある点において微分ができるかどうかであり,その判別は定義に従って左右極限を考えましょう。また,連続性と微分可能性の関係性についても以下の記載の内容を正確に理解しなければなりません。
- 連続である …… グラフが繋がる
- 微分可能である …… グラフが滑らかに繋がる
また,詳細は微積分の基本定理で述べますが,微分と積分の関係性についても把握しておきましょう。
微分可能性

微分と積分の関係

微分計算
ここでは微分可能な関数の微分計算の方法について解説しています。基本関数の微分公式を正確に使いこなすとともに,商の微分法,合成関数の微分法,対数微分法,陰関数微分,逆関数の微分について使いどころを理解していきましょう。
- 商の微分法 …… 割り算の微分方法
- 対数微分 …… 指数形や積の形
- 陰関数微分 …… 二次曲線でよく使います
- 逆関数の微分 …… 逆関数が求まらない場合の微分法
微分計算

基本関数の微分

微分の演算

合成関数の微分

対数微分

陰関数微分

逆関数の微分

微分による傾き・接線・法線の扱い
大学入試では,微分を用いて曲線の接線や法線を扱う問題は非常に多く出題されます。こうした問題では微分計算でのミスや,接線法線の方程式を作る際の計算ミスがあると,大問の多くの得点を落とすことになるため,大いに計算ミスに注意してください。また,接線の本数と接線の個数の対応についても重点的に注意を払うようにしましょう。最後に,2曲線の扱いについては円とそれ以外で異なりますので,使い分けられるようにしてください。
接線・法線
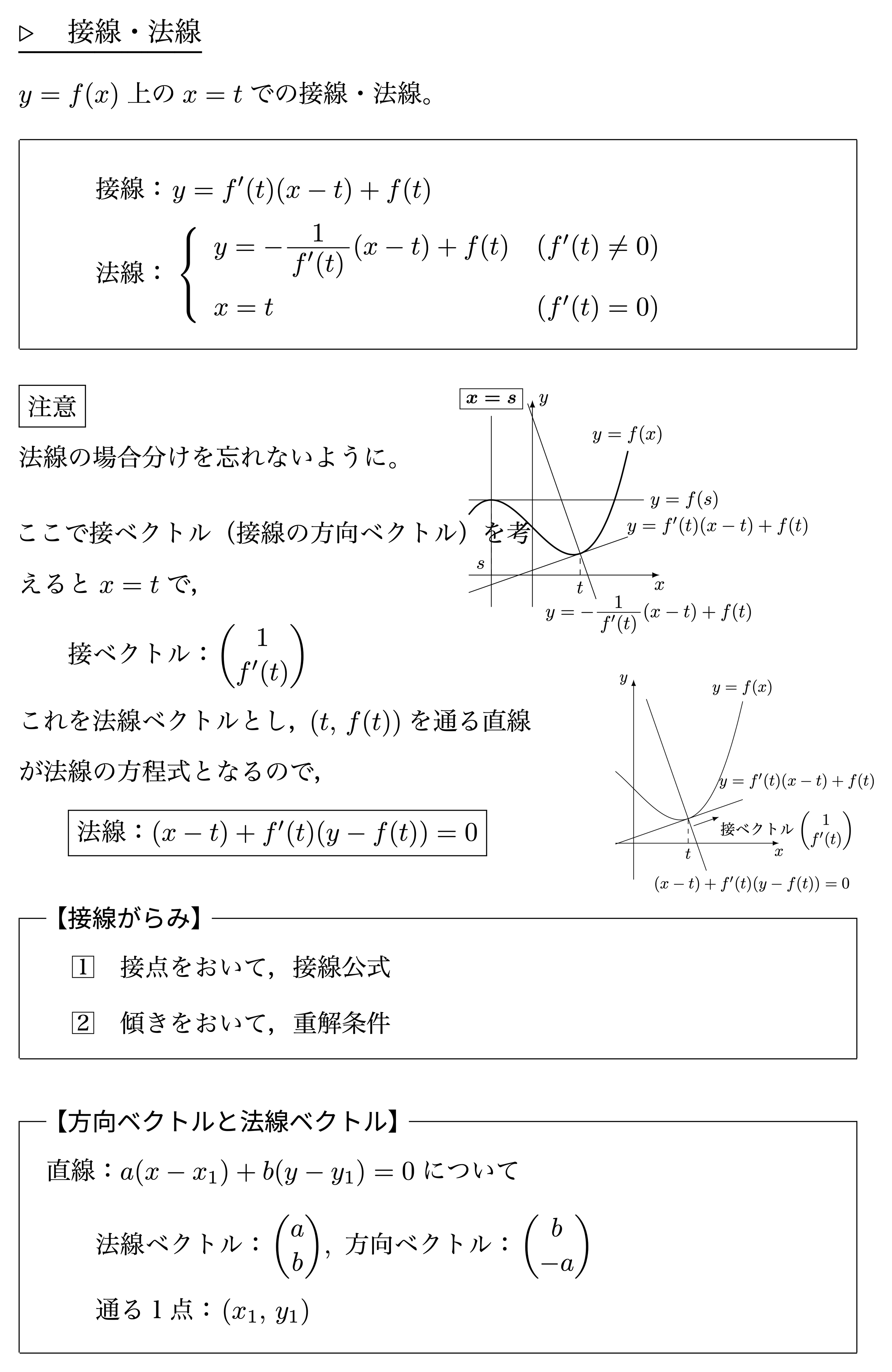
接線の本数

共通接線

4次関数の自己共通接線

2曲線の扱い
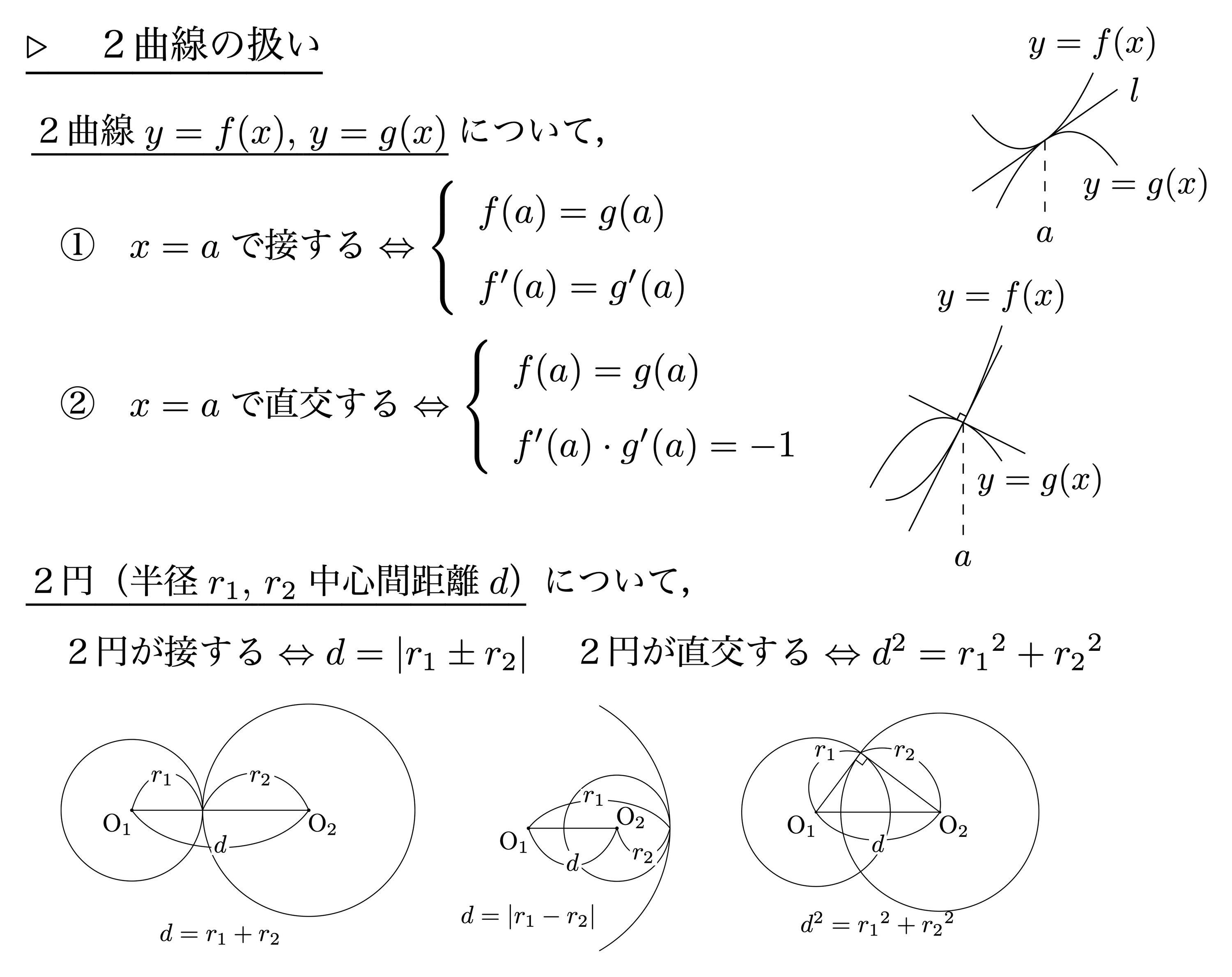
微分とグラフの関係
関数についての単調性・極値・凸性・変曲点についての説明をしています。単調性や凸性については正確な定義を理解するとともに,さらに微分を用いた議論をできるようにしていきましょう。併せて,極値や変曲点についても増減表を用いて考えられるようにし,グラフを描くことができるようにしてください。ただし,グラフには概形と詳細なものとの2種類があり,それぞれによって扱いが異なりますので,以下の説明をよく読んでください。
単調性

極値

凸性と凸不等式

変曲点

凸性を含むグラフの描き方
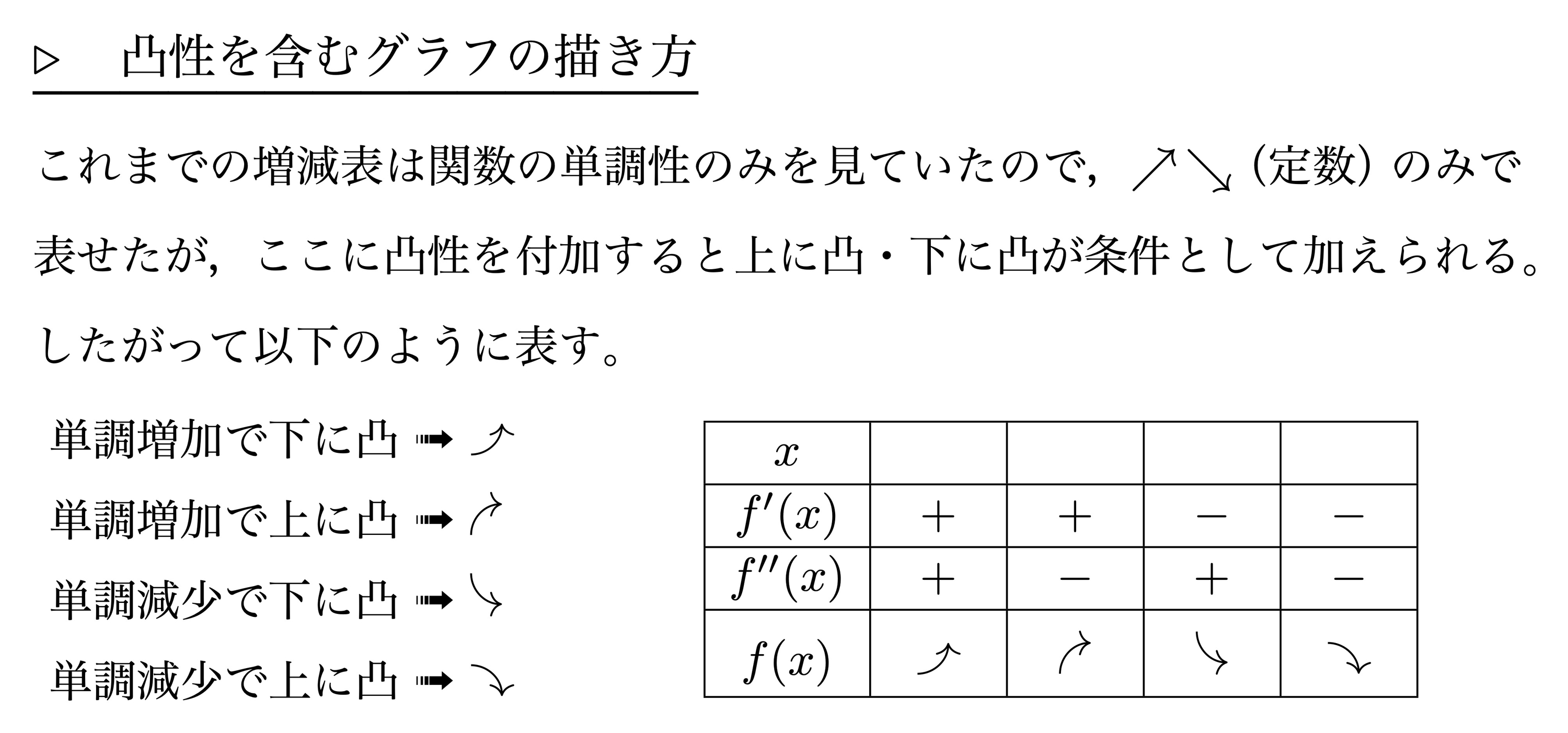
グラフの描き方

漸近線

パラメータ微分
パラメータ表示関数についての微分,パラメータ微分を扱います。パラメータの増減に伴う$x, y$の動きをパラメータ微分で考えます。また,対称性の活用をすることで増減表の範囲を制限し,解答を簡略化していきましょう。
パラメータ微分

パラメータ微分のグラフ
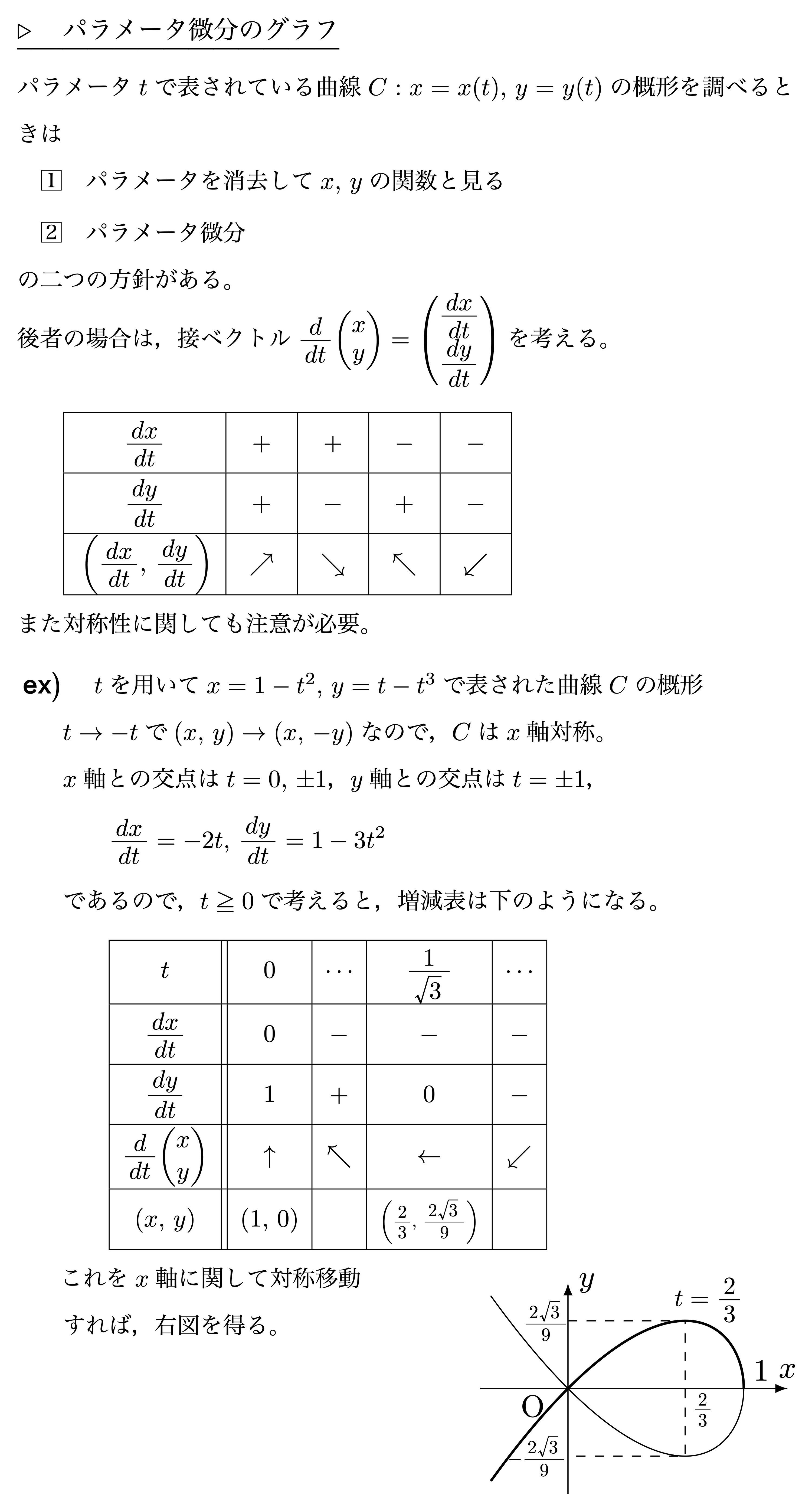
パラメータ分離
2つ上で扱ったグラフの描き方を利用することで,パラメータを含む方程式や不等式の解法として,パラメータ分離を用いることができます。これは,与えられたパラメータを含む方程式や不等式について,パラメータ単体を移項して,方程式の解の問題をグラフの共有点の議論に言い換えることです。
パラメータ分離

最大最小
ここでは,入試で頻出の最大最小問題の解法の説明をしています。出てくる考え方は,
- 文字消去
- 置換
- 文字固定
- 逆像法
- 有名不等式
になります。図形問題では初めの変数の取り方次第で(微分)計算の煩雑さが変わってくることにも注意しましょう。
多変数関数の最大最小

図形量の最大最小

不等式証明

中間値の定理・平均値の定理
ここでは中間値の定理と平均値の定理について説明しています。両者を混同しがちな人が多いと思いますので,しっかりと整理しておきましょう。中間値の定理は解の存在を述べるために利用し,平均値の定理は不等式証明に利用することがほとんどです。以下の詳細を読み,使いこなしてください。
中間値の定理

Lagrangeの平均値の定理

