数III毎日計算ドリル 19日目
解答
問1 次の極限を求めよ。\[\displaystyle \lim_{x\to0}(\cos x)^{\frac{1}{\sin^2x}}\]
【解答】
$\displaystyle -\frac{\pi}{2}<x<\frac{\pi}{2}$ で $(\cos x)^{\frac{1}{\sin^2 x}}>0$ より,$\log$ をとって,
\begin{align*}
&\lim_{x\to0}\log(\cos x)^{\frac{1}{\sin^2 x}}\\[6pt]
={}&\lim_{x\to0}\frac{\log(\cos x)}{\sin^2 x}\\[6pt]
={}&\lim_{x\to0}\frac{\log(1+(\cos x-1))}{\cos x-1}\frac{\cos x-1}{\sin^2 x}\\[6pt]
={}&\lim_{x\to0}\frac{\log(1+(\cos x-1))}{\cos x-1}\frac{-1}{1+\cos x}\\[6pt]
={}&-\frac{1}{2}\\[6pt]
={}&\log e^{-\frac{1}{2}}
\end{align*}
対数関数の連続性から,$\displaystyle \lim_{x\to0}(\cos x)^{\frac{1}{\sin^2 x}}=\boldsymbol{\frac{1}{\sqrt{e}}}$
最後の極限計算の部分では,符号に気を付けて極限公式を利用しています。
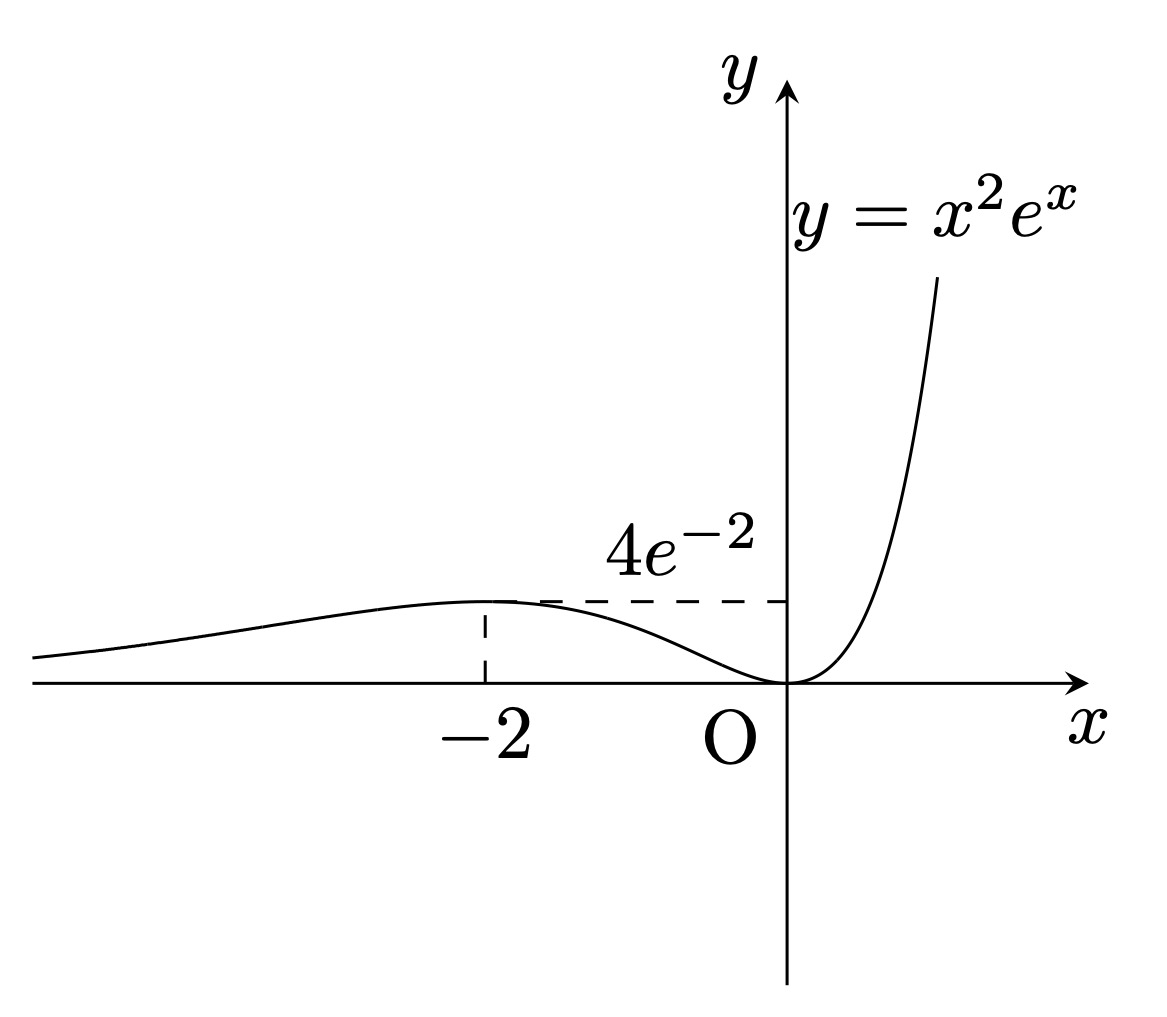
問2 次のグラフの概形を描け。\[y=x^2e^{x}\]
【解答】
極値は参考のために載せている。
\begin{align*}
\left\{\begin{array}{l}
\lim_{x\to-\infty}x^2e^{x}=+0\\[6pt]
\lim_{x\to\infty}x^2e^{x}=\infty
\end{array}\right.\text{}
\end{align*}
と自明解 $x=0$ よりグラフは次の通り。
問3 次の積分を計算せよ。\[\int\frac{dx}{x(x+1)^2}\]
【解答】
$\displaystyle\frac{1}{x(x+1)^2}=\frac{1}{x}-\frac{1}{x+1}-\frac{1}{(x+1)^2}$ と部分分数分解して,
\begin{align*}
&\int\frac{dx}{x(x+1)^2}\\[6pt]
={}&\int\left(\frac{1}{x}-\frac{1}{x+1}-\frac{1}{(x+1)^2}\right)\ dx\\[6pt]
={}&\boldsymbol{\log\left|\frac{x}{x+1}\right|+\frac{1}{x+1}+C}
\end{align*}
ただし,$C$は積分定数とする。
