数III毎日計算ドリル 24日目
解答
問1 次の極限を求めよ。\[\displaystyle \lim_{x\to\infty}(1+x)^{\frac{1}{x}}\]
【解答】
$\log$をとって,
\begin{align*}
\lim_{x\to\infty}\log(1+x)^{\frac{1}{x}}
&=\lim_{x\to\infty}\frac{\log(1+x)}{x}\\
&=0\\
&=\log 1
\end{align*}
対数関数の連続性から,$\lim_{x\to\infty}(1+x)^{\frac{1}{x}}=\boldsymbol{1}$
$e$の定義を使うタイプとは違うので要注意!!
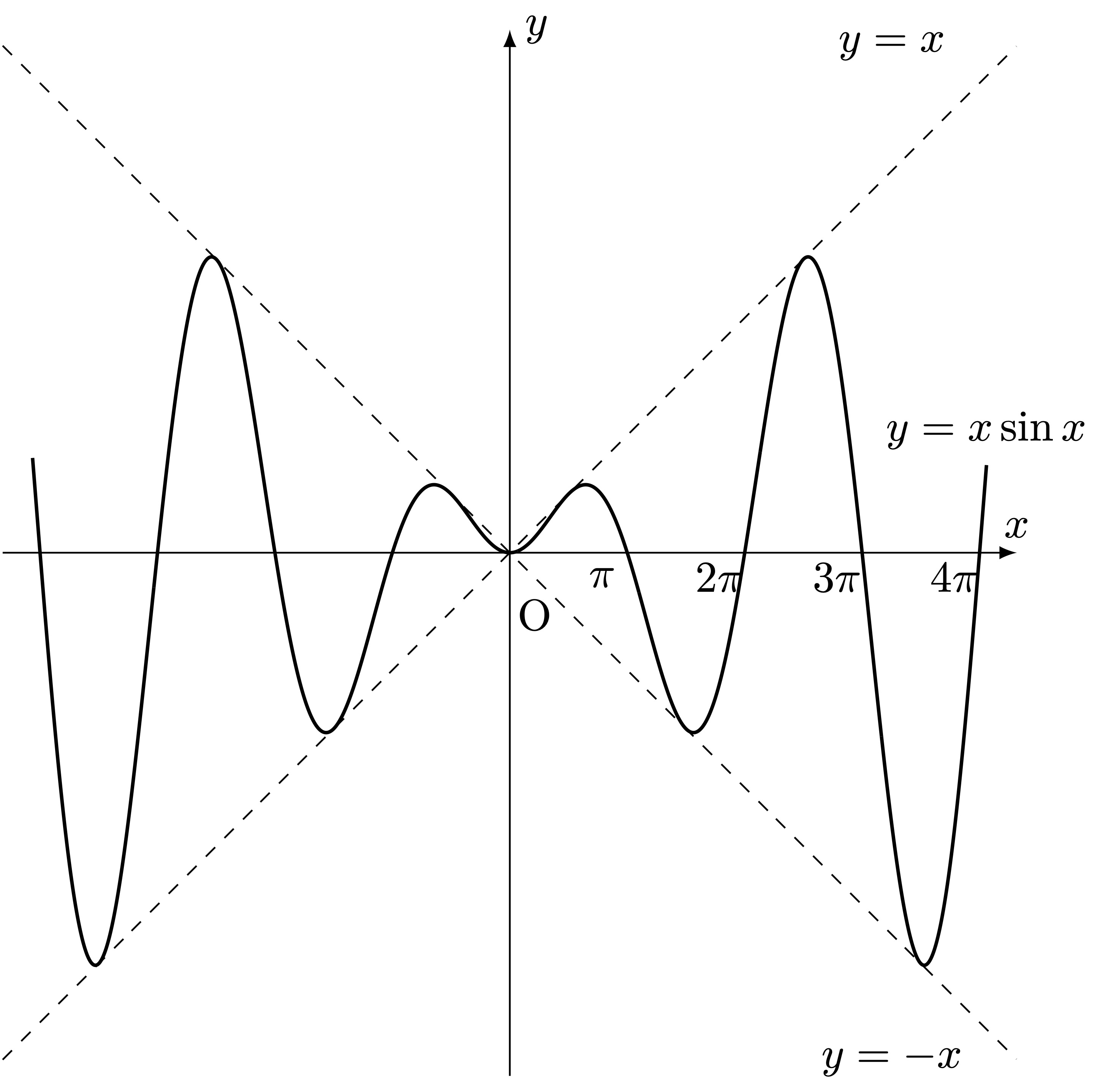
問2 次の関数のグラフの概形を描け。\[\displaystyle y=x\sin x\]
【解答】
$y=f(x)\sin x,\quad y=f(x)\cos x$のグラフは,$y=\pm f(x)$のグラフを点線で描いたのちに,その間に$\sin$カーブや$\cos$カーブを接するように描く。ただし,$y=f(x)$の偶奇性と$\sin$が奇関数で$\cos$が偶関数であることに注意。
今回は $y=\pm x$ を点線で描き,$y=\pm x$ が奇関数で $y=\sin x$ が奇関数なので $y=x\sin x$ が偶関数となり $y$軸対称に内部にカーブを描く。
問3 次の積分を計算せよ。\[\int_0^1\frac{dx}{x^2+x+1}\]
【解答】
与式はこれ以上次数下げできず,部分分数分解も無理なので,分母の置換を行う。
$\displaystyle x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}$であるので,
$\displaystyle x+\frac{1}{2}=\frac{\sqrt{3}}{2}\tan\theta\ \left(-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right)$とすると,
$\displaystyle dx=\frac{\sqrt{3}}{2\cos^2\theta}d\theta$ と,$\displaystyle x:0\to1$ で $\displaystyle \theta:\frac{\pi}{6}\to \frac{\pi}{3}$より,
\begin{align*}
(与式)&=\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{1}{\displaystyle \frac{3}{4}(1+\tan^2\theta)}\frac{\sqrt{3}d\theta}{2\cos^2\theta}\\[6pt]
&=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{2}{\sqrt{3}}d\theta\\[6pt]
&=\boldsymbol{\frac{\sqrt{3}\pi}{9}}
\end{align*}
