数III毎日計算ドリル 29日目
解答
問1 次の極限を求めよ。\[\displaystyle \lim_{x\to 0}\frac{\tan 2x^2}{(e^{3x}-1)\log(1-x)}\]
【解答】
\begin{align*}
&\frac{\tan 2x^2}{(e^{3x}-1)\log(1-x)}\\[6pt]
={}&-\frac23\cdot\frac{\tan 2x^2}{2x^2}\cdot\frac{3x}{e^{3x}-1}\cdot\frac{-x}{\log(1-x)}\\[6pt]
\to{}&\boldsymbol{-\frac23}\quad(x\to 0)
\end{align*}
最後の極限計算の部分では,符号に気を付けて極限公式を利用しています。
問2 $y=\sqrt{4x^2-x}$ のグラフの概形を描き,漸近線を記せ。
【解答】
極値は参考のために載せている。
\begin{align*}
y'&=\frac{x-2}{\sqrt[3]{x(x-3)^2}}\\
y''&=-\frac{2}{x(x-3)\sqrt[3]{x(x-3)^2}}
\end{align*}
であり,$y=0$のとき$x=0,\,3$で,
\[\lim_{x\to\pm\infty}\{y-(x-1)\}=\cdots=0\]
となるから,漸近線は$y=x-1$であり,増減表は下のようになる。
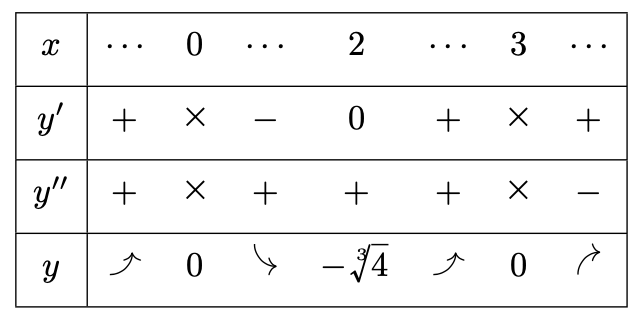
以上からグラフは次の通り。
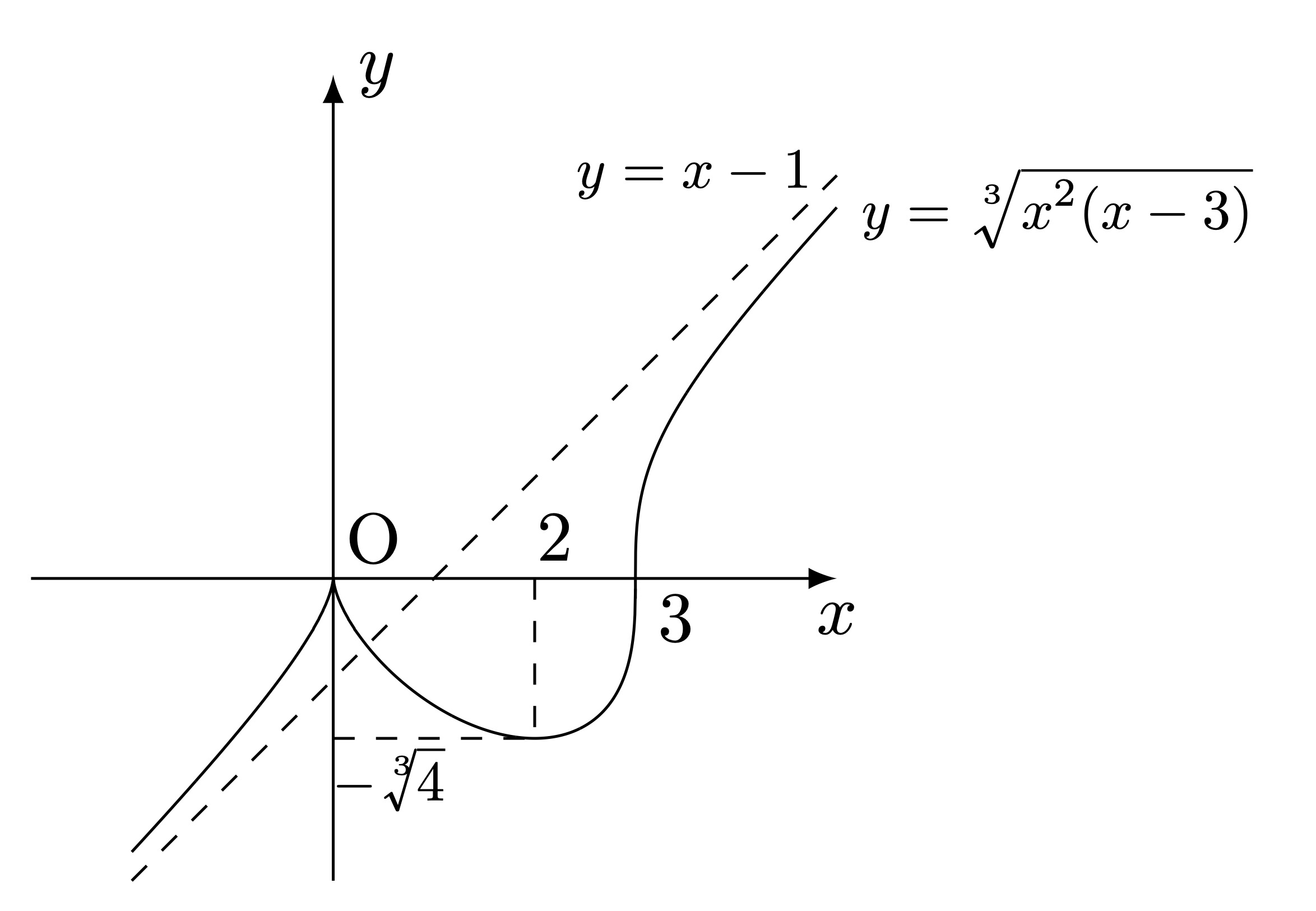
【注意】
この関数は$x=0,\,3$で微分可能でない。
問3 次の積分を計算せよ。\[\int_0^1\frac{4x+2}{2x^2+5x+2}\ dx\]
【解答】
微分形と部分分数分解を考えて,
\begin{align*}
&\int_0^1\frac{4x+2}{2x^2+5x+2}\ dx\\[6pt]
={}&\int_0^1\frac{(2x^2+5x+2)'-3}{2x^2+5x+2}\ dx\\[6pt]
={}&\int_0^1\frac{(2x^2+5x+2)'}{2x^2+5x+2}\ dx-\int_0^1\frac3{(2x+1)(x+2)}\ dx\\[6pt]
={}&\int_0^1\frac{(2x^2+5x+2)'}{2x^2+5x+2}\ dx-\int_0^1\left(\frac2{2x+1}-\frac1{x+2}\right)\ dx\\[6pt]
={}&\Bigl[\log|2x^2+5x+2|-\log|2x+1|+\log|x+2|\Bigr]_0^1\\[6pt]
={}&\boldsymbol{2\left(\log3-\log2\right)}
\end{align*}
分数関数の積分の復習は,こちらを参照してください!
