積分
Riemann積分の定義の説明や不定積分/定積分の説明をした上で,微分との関係性を解説しています。
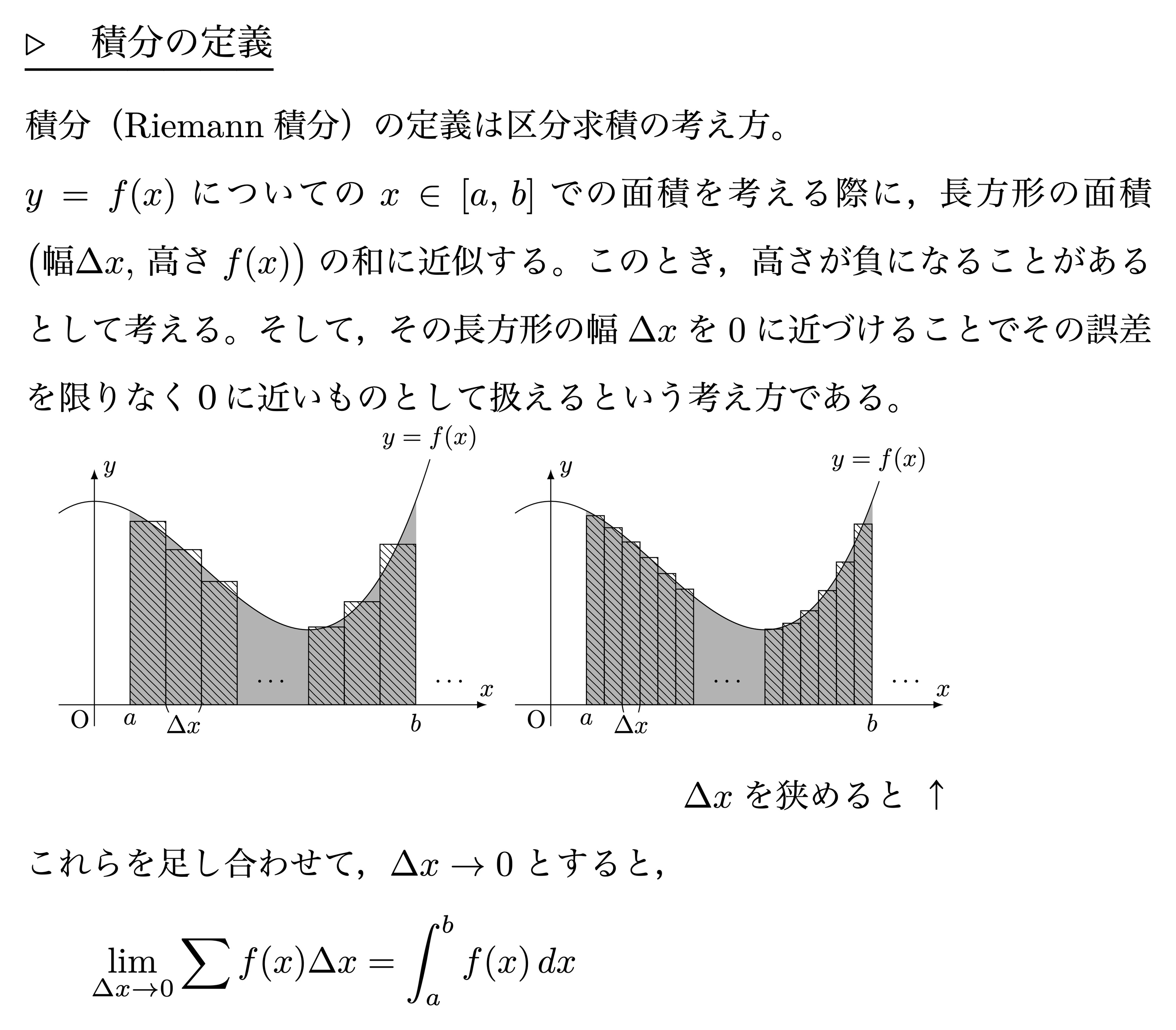
積分の定義
不定積分

微積分の基本定理

定積分

不定積分
まずは不定積分についての説明です。基本関数の積分公式を使いこなすことはもちろんですが,公式を使う前の式変形が重要になってきます。また,微分形を見つけて利用することで簡単に計算することができますので,マスターしていきましょう。
不定積分計算

基本関数の積分

不定積分の演算
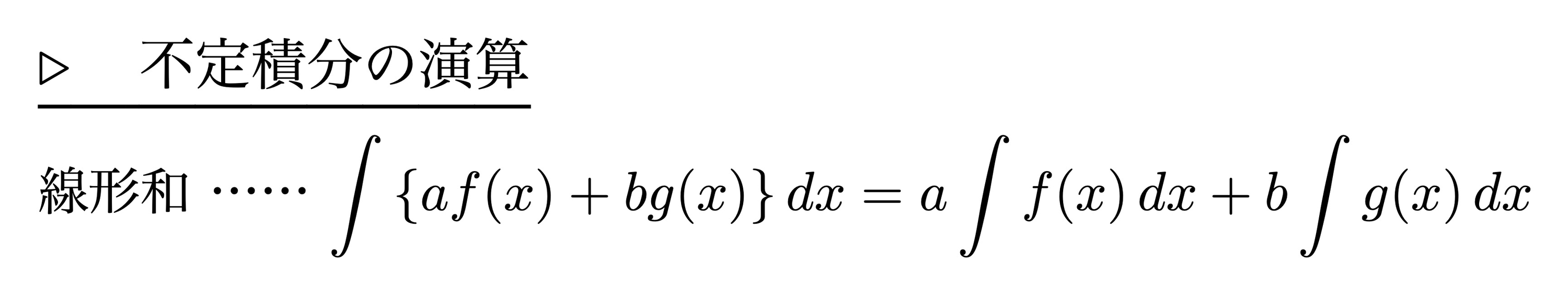
微分形の利用

定積分
定積分では,上の不定積分の計算方法に加えて,更なる工夫や式に合わせた処理が必要になってきます。まずは,定積分の特徴である積分区間の存在による対称性や周期性を利用するもの。次に,無理関数・三角関数・分数関数・絶対値関数などの式の形に合わせて,ある程度式変形の処理の方向性が定まります。いずれも入試問題において積分計算としての出題だけに留まらず,面積体積などの計算に絡めて頻出ですので,必ず計算できるようにしていきましょう。
定積分の公式

定積分計算

偶関数と奇関数の積分

絶対値関数の積分

置換積分
置換積分とは,積分の中身,被積分関数の中の一部分をかたまりと見て文字を置き換えるワザです。もちろん,定積分と不定積分によって扱いに違いがあるため,使い分けられるようにしましょう。また,置換積分の使い所としては,無理関数・指数関数・対数関数の積分が挙げられますので,一つ一つの代表例を見ておきましょう。
置換積分の手順

よくある置換積分

置換積分を利用した工夫
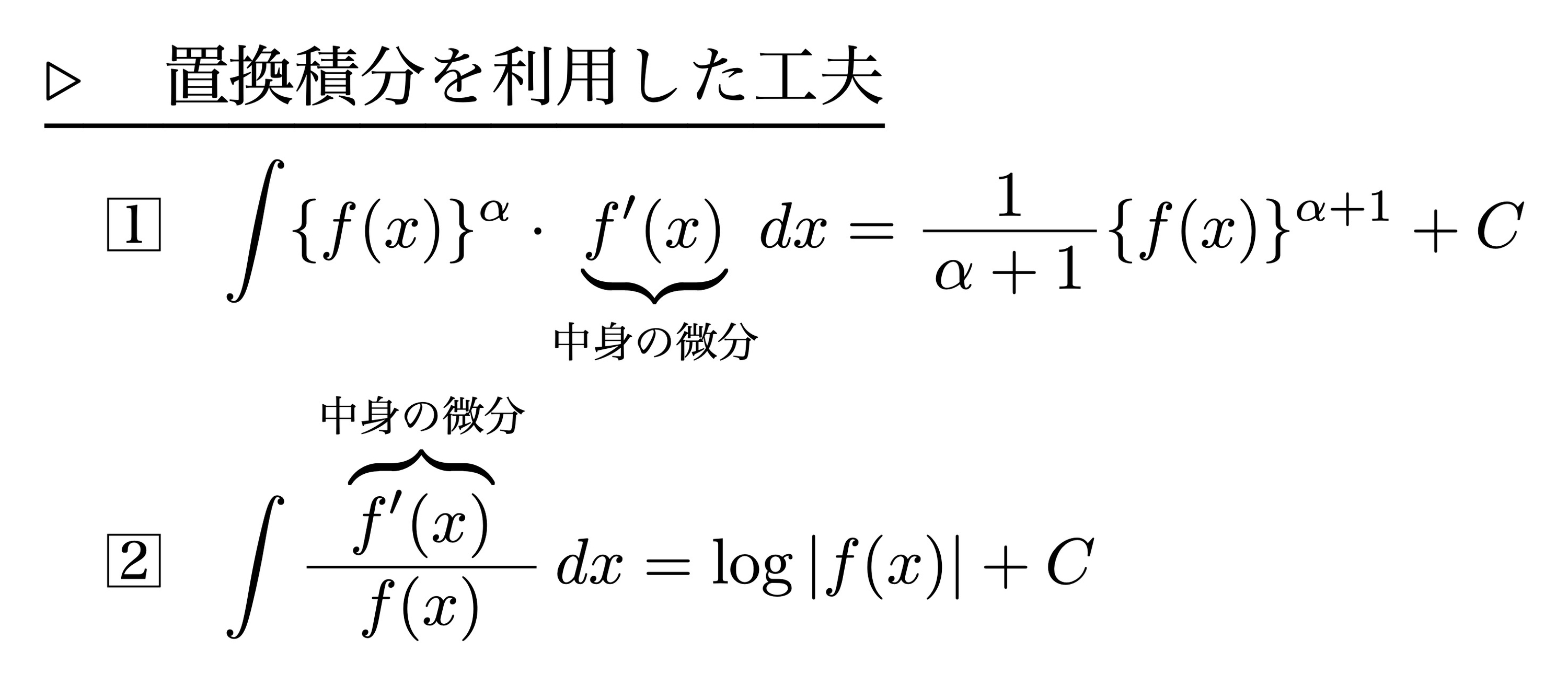
双曲線関数

部分積分
部分積分は,最強の積分手段の一つと言えるでしょう。積分の中身,つまり被積分関数が関数の積の形になっているときに利用します。「積分計算で行き詰まったら,部分積分しておけばなんとかなる」と言う人がいるほど有効的な方法ですので,必ず使いこなしましょう。鉄緑会での指導経験から,一般の教科書とは大きく異なる説明をしていますが,符号ミスや複数回の部分積分に対応するためには必ず以下の方法で考えることをオススメします。
微分を用いた部分積分

積分漸化式

各種関数の積分計算
各種関数の積分として,周期関数・べき展開・分数関数・無理関数の積分について説明しています。いずれも重要ですが,べき展開は数IIBにおける$\frac{1}{6}$公式の仲間であり受け入れやすいでしょう。分数関数と無理関数については,計算手法を覚えなければなりません。部分分数分解とその後の処理や,円を用いた考え方,置換の方法についてそれぞれ覚えて使いこなしてください。
周期関数の積分

べき展開

分数関数の積分

無理関数の積分

三角関数の積分
三角関数の積分は,数ある積分計算の中でも特に式に合わせた解法が多くあり,多くの練習を積んで使い分けることを目指しましょう。次数下げ・部分積分・置換積分だけではなく,定積分では面積の利用など様々な解法があります。
三角関数の不定積分

三角関数の定積分

面積積分
積分を用いて面積を求めることを考えましょう。考え方はRiemann積分の定義と同じであり,曲線によって囲まれた部分を短冊状に切って長方形の面積の和として考えます。ポイントは,必ずグラフを描いて考える習慣をつけることです。また,難しい問題では積分区間である交点の座標が求まらない場合は,関係式をおいて考えましょう。べき展開による$\frac{1}{6}$公式の仲間を覚え,逆関数が求まらない場合の面積では置換を利用する方法を覚えましょう。積分を用いて面積を考えるとき,その式は絶対値関数の積分の形となります。そこで,絶対値関数の積分の最大最小の問題において面積を利用して考える方法,変分法(はみ出し削り論法と呼ぶ人もいる)を用いると答えがすぐに見えることを覚えてください。
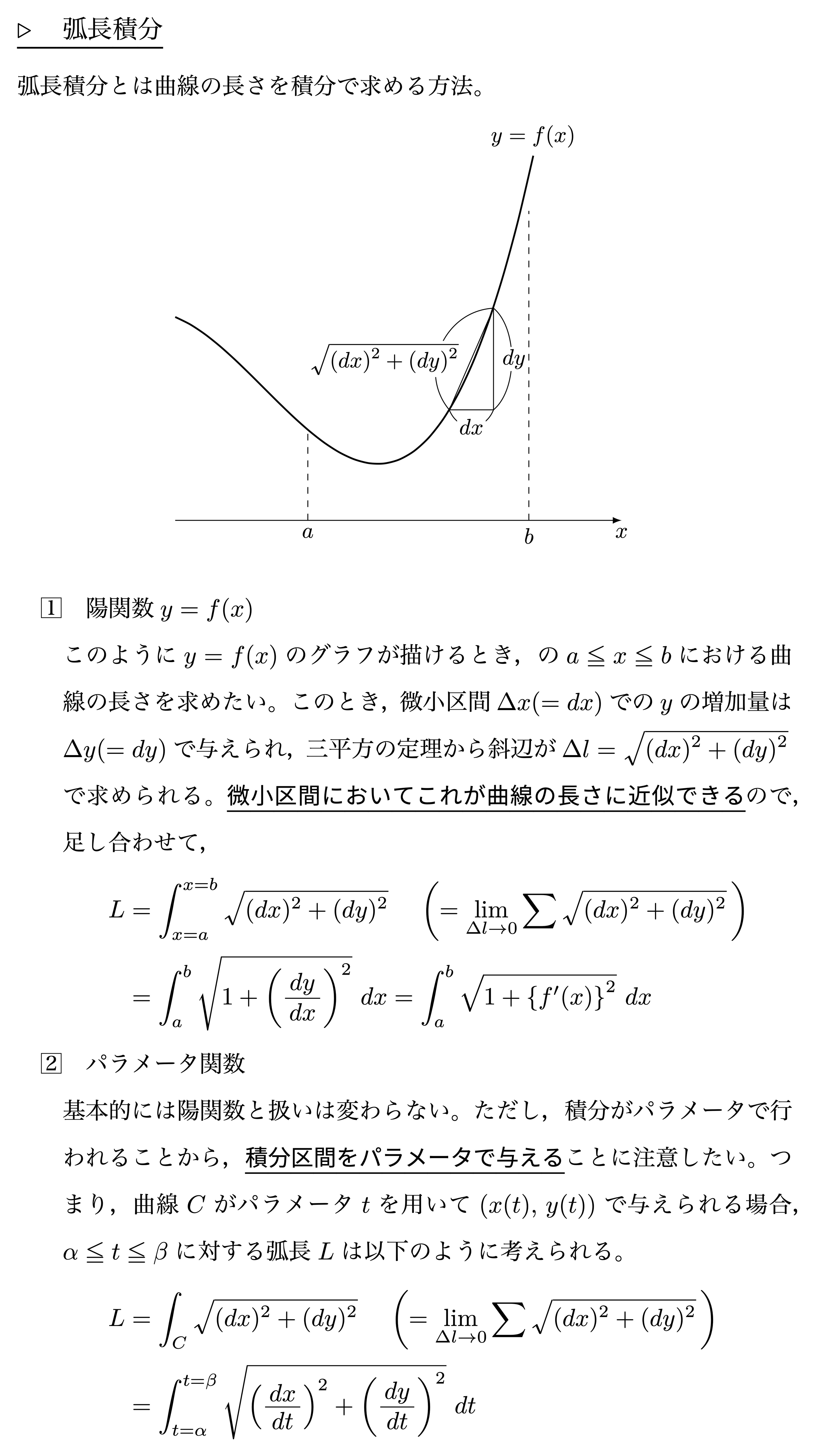
弧長積分
曲線の長さについては,$y=f(x)$の形のみではなくパラメータ表示の関数についても求められるようにしましょう。導出を考えれば簡単に求めることができます。
弧長積分
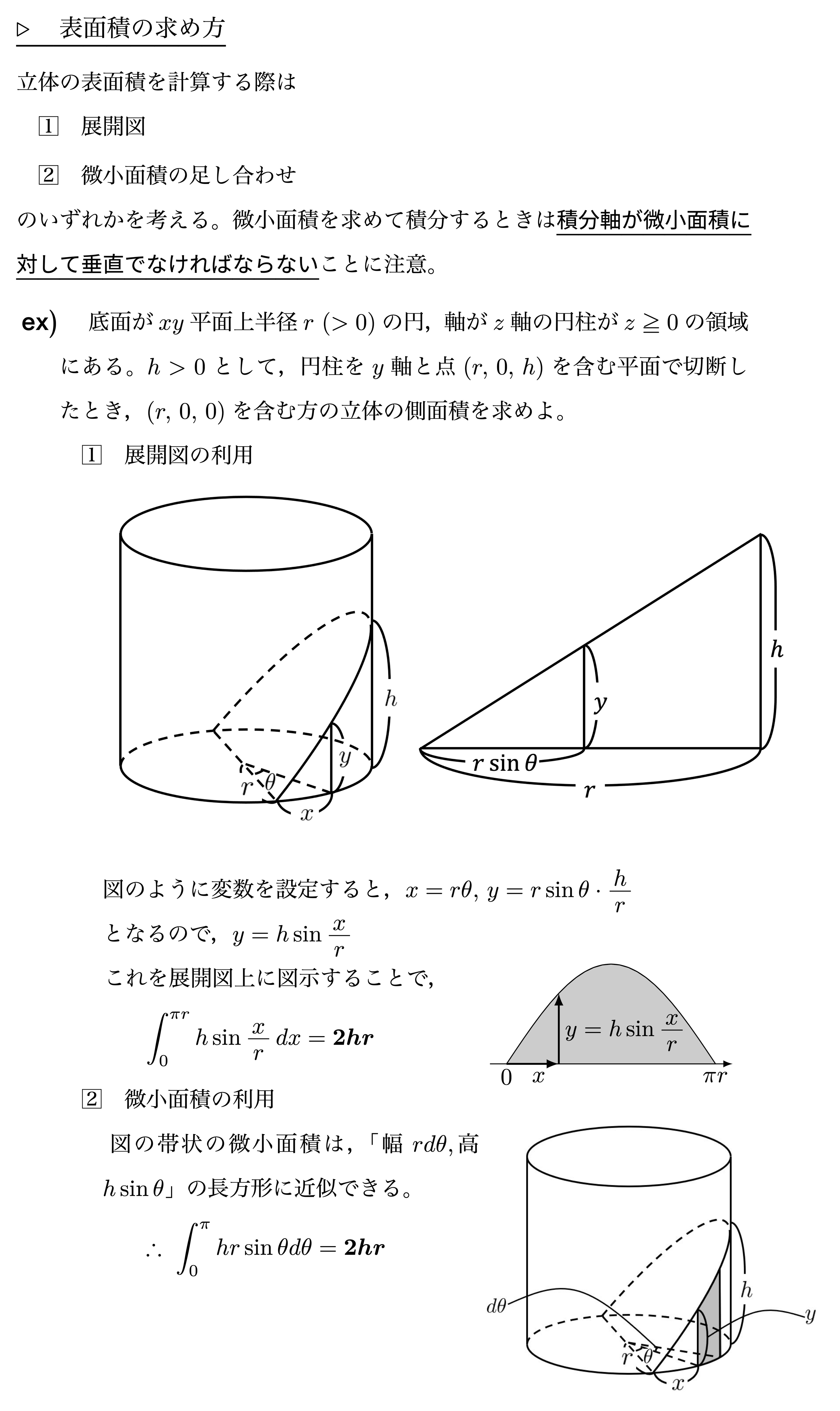
体積積分
積分を用いて体積を求めるイメージは,高さが非常に薄い断面積を積み重ねて全体の体積を求めるというものです。つまり,断面積を積分によって足し合わせるのですが,重要なことは「断面積」「積分軸」にあります。この2点はいずれかが定まればおのずと他方も決定されるわけですが,
- 回転体 …… 断面は円かドーナツ → 回転軸が積分軸
- 非回転体 …… 求めやすい断面積 → 断面に垂直に積分軸
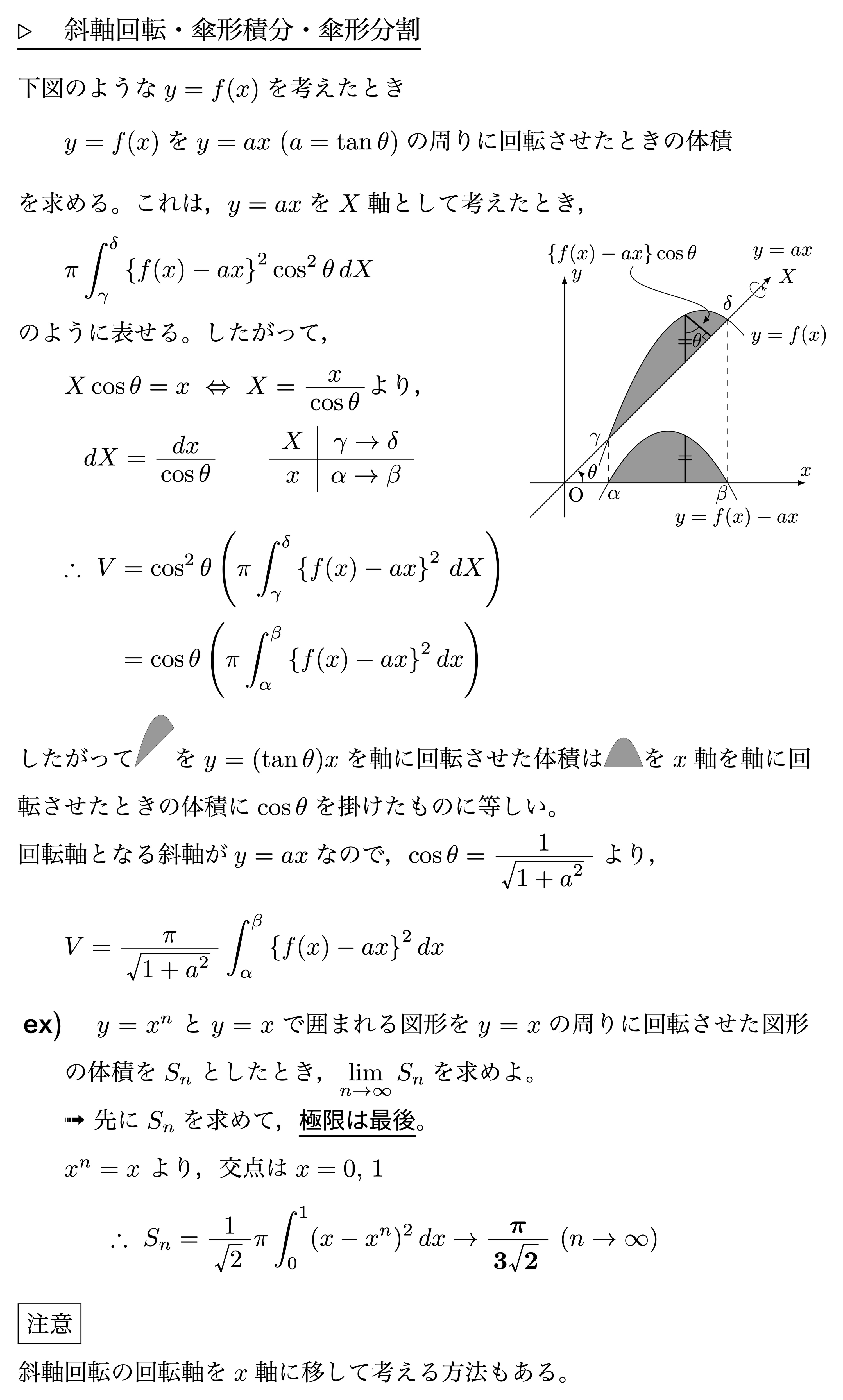
のように,回転体と非回転体で多少の違いがあることを理解しておきましょう(非回転体は自分で断面の形を考えなければならないが,回転体は必ず円やドーナツ形)。また,逆関数が求まらない場合の考え方である円筒近似や,回転軸が斜めの斜軸回転,共通部分の体積などについてもしばしば出題されますので一通り覚えてください。
パラメータ積分
パラメータ表示関数についての面積や体積について積分を用いて考える際には,もちろんグラフを描いたあと,
- $x, y$で立式
- 全てパラメータに置換
の手順で解答できます。必ず区間が繋がることに注意して計算ミスに気づきましょう。極方程式で考えられるものについては,扇形近似の利用も考えてください。
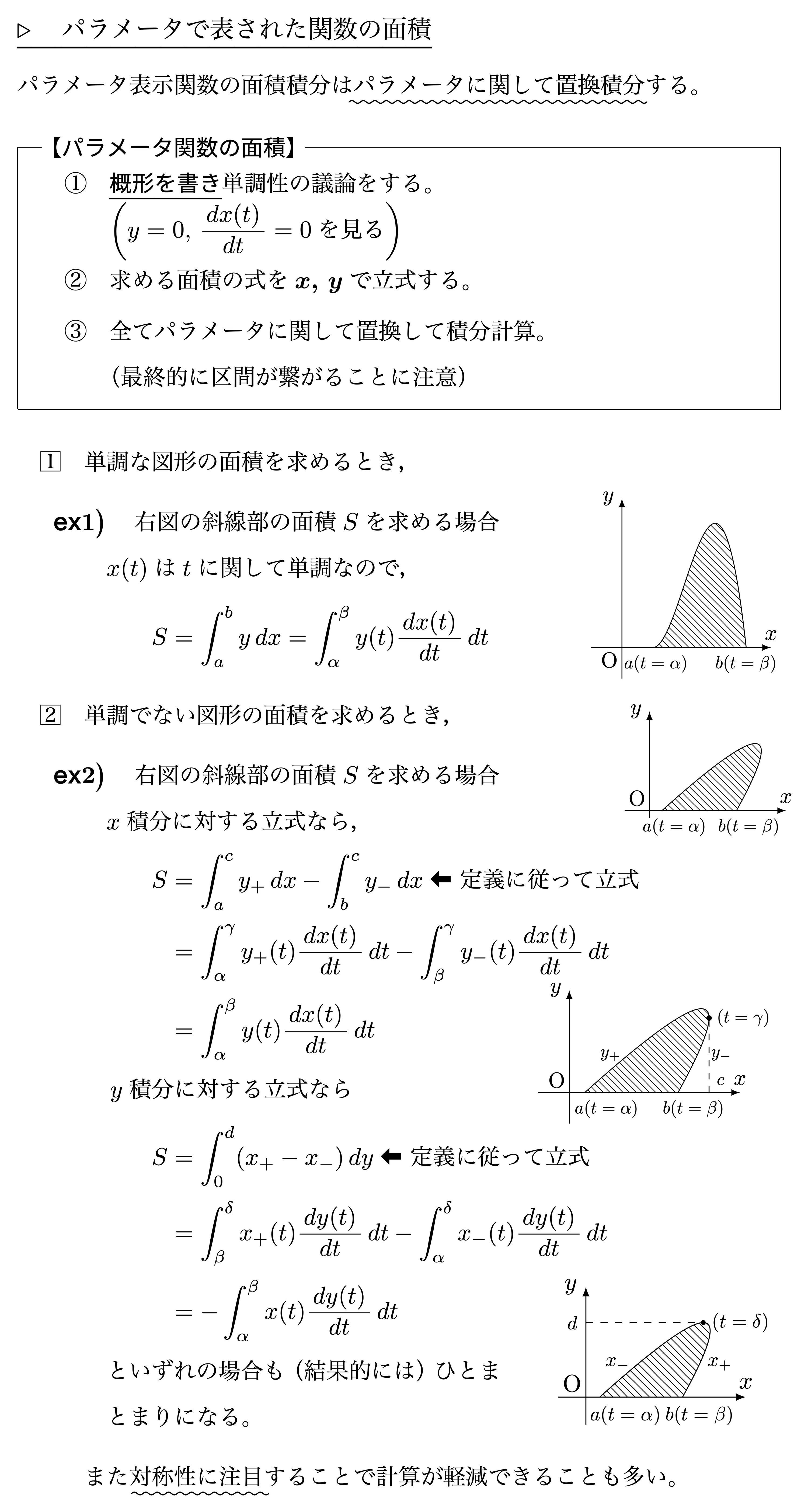
パラメータで表された関数の面積
パラメータで表された関数の体積

積分方程式
積分方程式は,式の形から2種類の判別をした後に,それぞれの解法に従うのみです。ただし,見慣れない微分方程式を解かねばならないものもありますので,変数分離法などの理解もしておくと良いかもしれません。変数分離法とは,微分方程式において,左辺と右辺に2つの変数を完全に分離して両辺を積分して扱う方法です。また,解答の中で微積分の基本定理を利用しますので,不安な人は見直しておきましょう。
積分方程式

定積分と不等式
定積分についての不等式証明の問題の解法は,ヒントが積分区間と積分変数です。
- 示したい不等式の形と区間から積分する関数を考える。
- (極限がらみで)複数の変数を持つ場合には,積分変数から積分する関数を考える。
加えて,極限が続くような問題では,示した不等式を利用してはさみうちの原理を用いることがほとんどです。
定積分と不等式
無限級数と積分

limΣの扱い
極限の問題ではあるものの,$\lim\sum$が$\int$であることを考えれば,これを積分の問題と捉えることができるでしょう。考え方は,以下に記しています。そのまま求める方法や区分求積法の2つは基本です。面積評価については少し難しいかもしれませんが,よく出題されますので覚えておきましょう。
和の極限の扱い

区分求積法

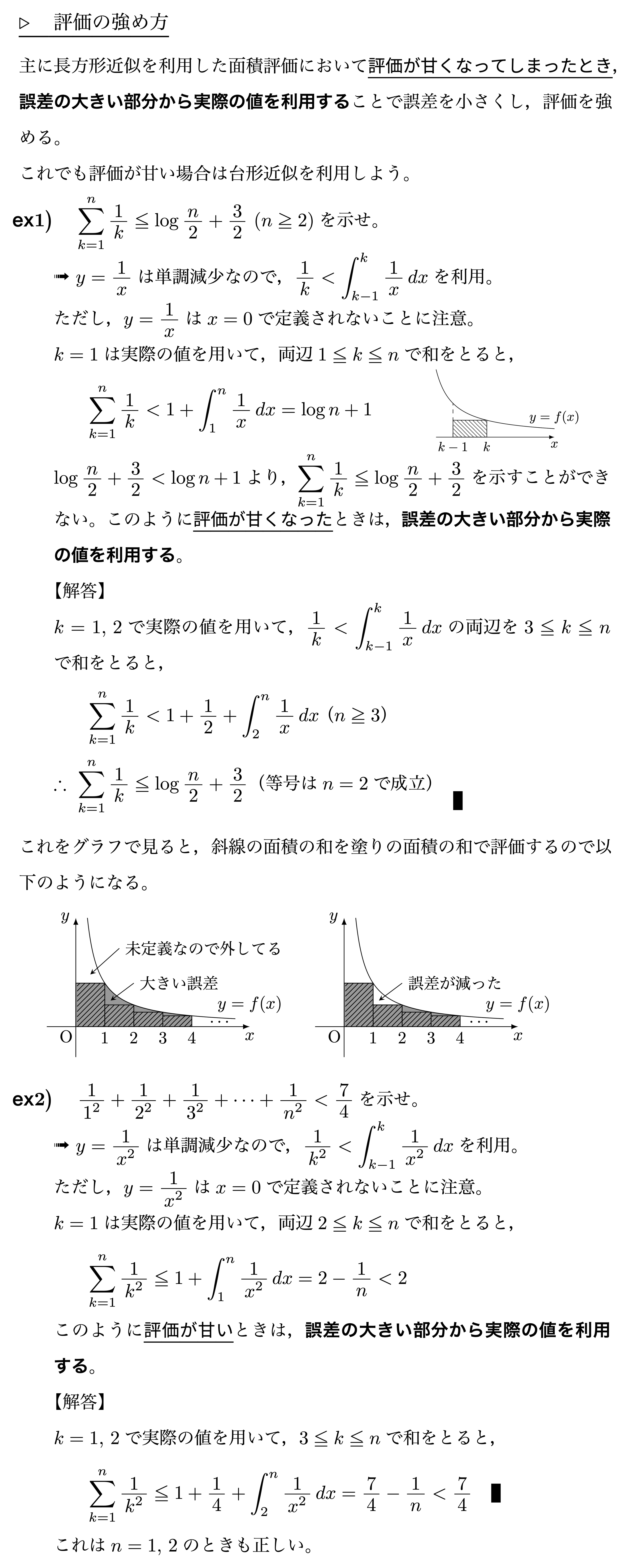
面積評価

長方形近似
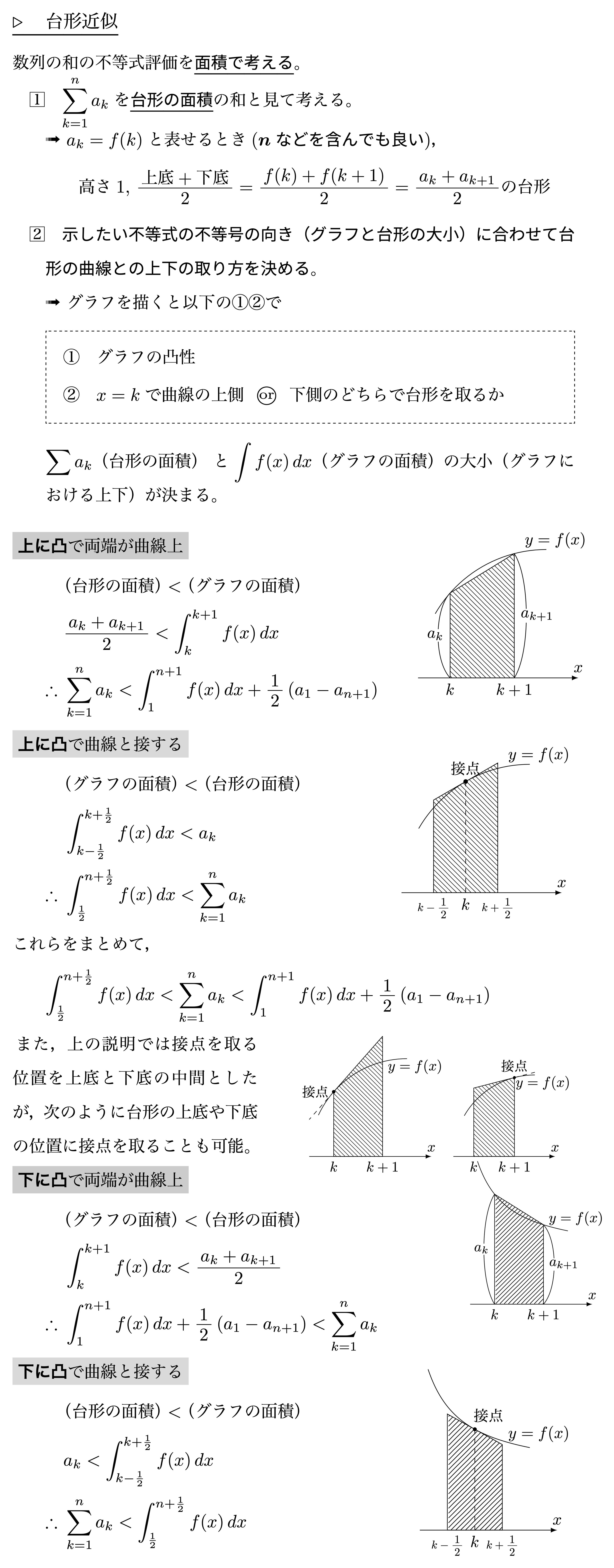
台形近似
評価の強め方