ベクトルの基本
ここではベクトルの基本として,その表記や座標とのつながりなどの説明をしています。
ベクトルとは
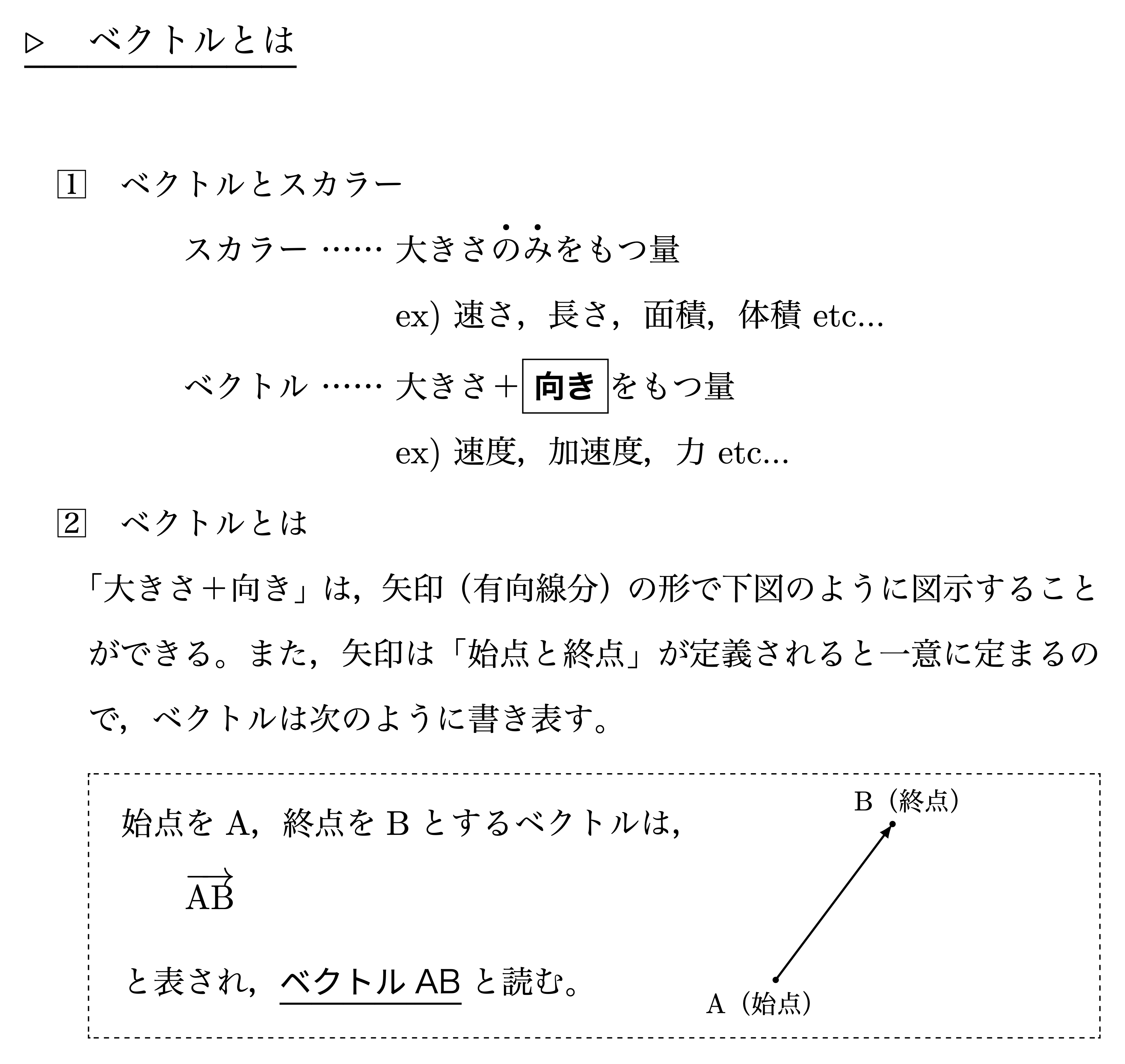
位置ベクトル

成分表示
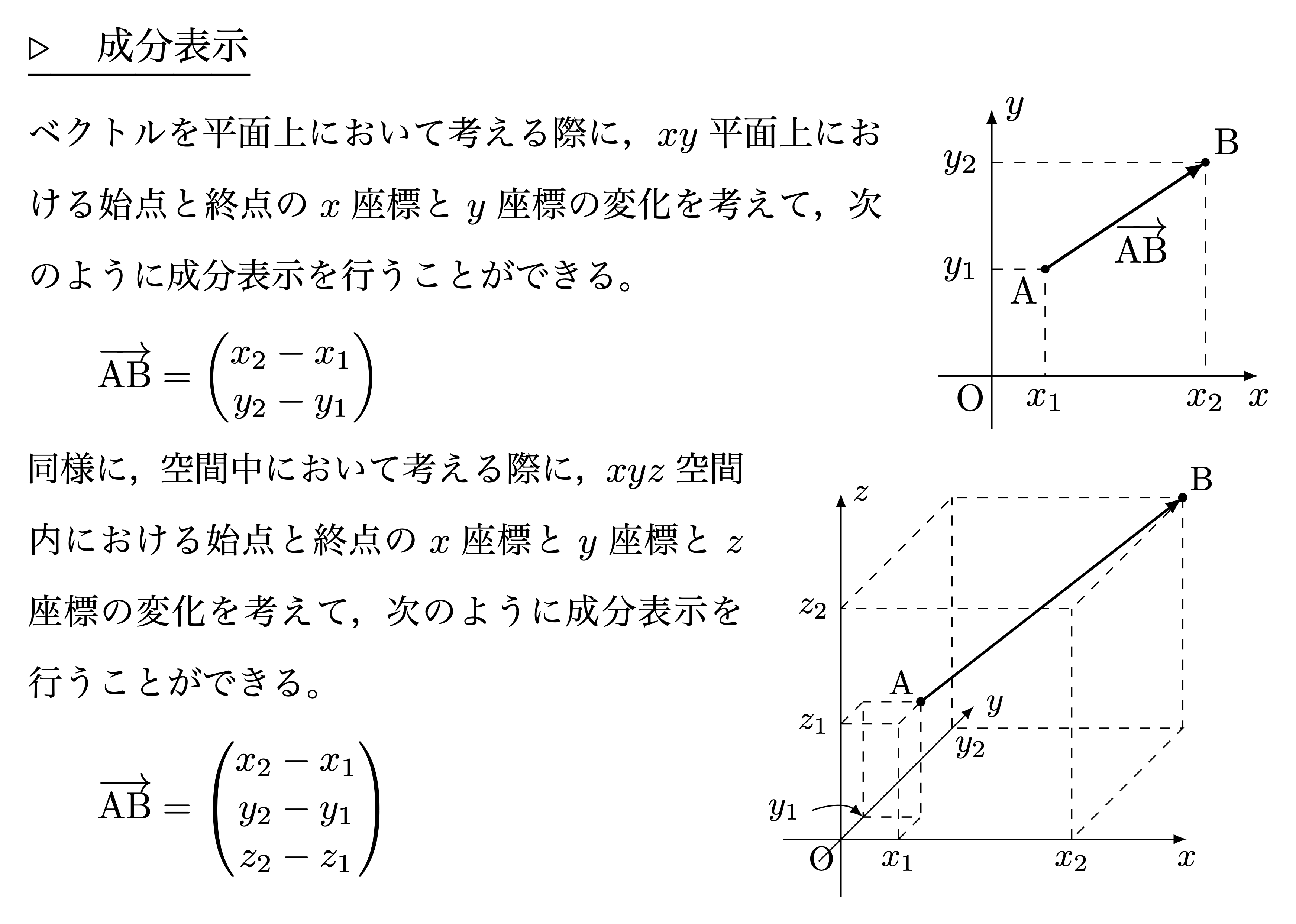
ベクトルの基本事項

ベクトルの演算
ベクトルの演算性質

ベクトルの和

ベクトルの実数倍

ベクトルの差
ベクトルの積

ベクトルの一次独立/一次従属
平面ベクトルの一次独立

空間ベクトルの一次独立

一次独立の利用

ベクトルの内積
ベクトルの内積

Cauchy - Schwarzの不等式
作成中
ベクトルの図形的な性質
図形的性質の平面と空間での違い

内分点・外分点

重心

三角形の面積公式

平行条件・直交条件

共線条件

共平面条件

方向ベクトル・法線ベクトル

ベクトルの外積
ベクトルの図形問題への利用
図形問題の解法一覧

ベクトルの終点範囲
平面ベクトルの終点範囲

空間ベクトルの終点範囲

斜交座標

ベクトル方程式
ベクトル方程式

直線のベクトル方程式

直線の方程式

平面のベクトル方程式

平面の方程式

円・球のベクトル方程式

円・球の方程式

ベクトル方程式の解法

射影
正射影ベクトル

正射影ベクトルの利用

